今回の記事では多管式熱交換器(シェル&チューブ式熱交換器)の設計計算の具体例について解説します。
プラントで使用される熱交換器で最もよく使用されるタイプは多管式熱交換器ですが、最近ではHTRI(Heat Transfer Research, Inc.)に代表されるソフトウェアを使用して設計することが一般的になっています。
業務の効率化のためには、このようなソフトウェアを駆使することは重要ですが、熱交換器の設計に慣れていないと、入力ミスや設計の前提に誤りがあっても気づかずにアウトプットを出してしまう可能性があるため、熱交換器の設計手順を知っておくことは重要です。
多管式熱交換器の一般的な設計手順は以下の通りです。
多管式熱交換器の設計手順
(1) 流路数の決定
(2) 管とシェルの流路数(パス数)の決定
(3) シェル径、バッフル間隔の決定
(4) 伝熱係数の計算
(5) 伝熱面積の決定
(6) 圧力損失の計算
(7) ノズル径、仕切り板などの決定
このような設計手順は機械設計エンジニアだけでなく、プロセスエンジニアも知っておく必要があります。
次項から、多管式熱交換器の設計計算の具体例について解説していきます。
合わせて読みたい
・【熱交換器】プラントで使用される熱交換器(Heat Exchanger)の種類と特徴の解説
・【熱交換器】熱交換器の77%ルールとは?安全弁設置基準について解説
・【熱交換器】空冷式熱交換器の設計の留意点について解説
・【熱交換器】多管式熱交換器(シェル&チューブ式)の流速、レイノルズ数の計算方法について解説
・【熱交換器】多管式熱交換器(シェル&チューブ式)の設計の留意点について解説
・【熱交換器】プレート熱交換器の設計の留意点について解説
・【熱交換器】二重管熱交換器の設計の留意点について解説
・【熱交換器】設計で使用されるU値(総括伝熱係数)と伝熱面積について解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
例題
流量が160m3/h、温度が70℃の苛性ソーダ水溶液を30℃まで冷却する多管式熱交換器を設計します。冷却水は10℃の冷水を使用するとします。
設計に必要な情報をまとめると、以下の通りとなります。
<高温側流体(苛性ソーダ)>
流量:160 [m3/h]
入口温度:70 [℃]
出口温度:30 [℃]
比熱:0.9 [kcal/kg ℃]
密度:1090 [kg/m3]
粘度:4.32 [kg/m h]
熱伝導度:0.54 [kcal/m h ℃]
<低温側流体(冷水)>
入口温度:10 [℃]
比熱:1.0 [kcal/kg ℃]
密度:1000 [kg/m3]
粘度:3.67 [kg/m h]
熱伝導度:0.5 [kcal/m h ℃]
流路の決定
冷水(低温側流体)の流量計算
どちらの流体を菅側にするかシェル側にするか決定するために、まずは冷水(低温側流体)の流量を計算します。
一般的に、熱交換器の経済的な設計のためには高温側流体と低温側流体との温度差(Temperature Approach)は10℃以上とすることが望ましいとされているため、冷水の出口温度は20℃とします。(低温側出口温度≦高温側入り口温度-10℃)
熱交換器の熱負荷(Duty)を計算すると、
$$Q=F_h*ρ_h*C_{ph}*ΔT_h$$
Q:熱負荷(Duty) [kcal/h]
ρh:高温流体密度 [kg/m3]
Fh:高温流体体積流量 [m3/h]
Cph:高温流体比熱 [kcal/kg ℃]
ΔTh:高温流体温度差 [℃]
より
Q=160*1090*0.9*40=6,278,400 [kcal/h]となります。
ここから、冷水側の比熱:1.0 [kcal/kg ℃]とΔT:10 [℃]、密度:1000 [kg/m3]を用いて流量を計算すると
$$F_C=\frac{Q}{ρ_c*C_{pc}*ΔTc}$$
Q:熱負荷(Duty) [kcal/h]
ρc:冷水密度 [kg/m3]
Fc:冷水体積流量 [m3/h]
Cpc:冷水比熱 [kcal/kg ℃]
ΔTc:冷水温度差 [℃]
より
Fc=6,278,400/(1,000*1.0*10)=627.84≒630 [m3/h]
となります。
流路の決定
この例題では、苛性ソーダの流量よりも冷水の流量が大幅に大きいことを考慮して、苛性ソーダを菅側、冷水をシェル側とします。
注意:実際には温度、圧力条件や腐食性、汚れの度合いなどを総合的に考慮して流路を決定します。流路の決定方法についてはこちらの記事を参照ください。
管とシェルの流路数(パス数)の決定
管本数の計算
多管式熱交換器の菅側では、圧力損失を過大にしないように、管内流速を1m/s~2.5m/sとすることが適切とされています。
ただし、あまり流速が小さすぎると伝熱係数も小さくなってしまうことに注意する必要があります。(目安としてRe数>10,000程度が必要)
今回は1.5m/sを採用することにします。
また、チューブ径については、こちらの記事では3/4"または1"と解説していますが、今回は1"(内径で27mm)を使用することにします。
$$N=\frac{F_h}{\frac{π}{4}d^2*u}$$
N:管本数
Fh:高温流体体積流量 [m3/h]=160 m3/h
d:管内径 [m]=0.027m
u:管内流速 [m/s]=1.5 m/s
上式から、N=160/(π/4*0.027*1.5)≒52本
となります。
伝熱面積(仮値)の計算
流路数(パス数)を決定するために、伝熱面積の概要(仮値)を計算しておきます。
注意:正確な伝熱面積は別途計算しますが、ここでは流路数(パス数)を求めて熱交換器の概要を決めるための計算です。
まず、対数平均温度差を計算すると、
$$ΔT_m=\frac{(T_{hi}-T_{co})-(T_{ho}-T_{ci})}{\ln\frac{T_{hi}-T_{co}}{T_{ho}-T_{ci}}}$$
Tm:対数平均温度差 [℃]
Thi:高温流体入口温度 [℃]=70℃
Tho:高温流体出口温度 [℃]=30℃
Tci:低温流体入口温度 [℃]=10℃
Tco:低温流体出口温度 [℃]=20℃
上式より、ΔTm=(50-20)/ln(50/20)≒33℃
となります。
ここで、総括伝熱経緯数(U値)は、流体が水であれば、500~1000 [kcal/m2 h ℃](1250~2500 [W/K m])程度ですが、今回は750 kcal/m2 h ℃として伝熱面積を計算すると、
$$A=\frac{Q}{UΔT_m}$$
A:伝熱面積(仮値) [m2]
Q:熱負荷(Duty) [kcal/h]=6,278,400 kcal/h
U:総括伝熱係数 [kcal/m2 h ℃]=750 kcal/m2 h ℃
Tm:対数平均温度差 [℃]=33℃
Tci:低温流体入口温度 [℃]=10℃
Tco:低温流体出口温度 [℃]=20℃
上式よりA=6,278,400/(750*33)≒254m2
となりました。
※パス数を決定するための仮の伝熱面積
必要管長の計算
上記の計算で、管の本数、伝熱面積が求められたため、必要管長は以下の計算式で求められます。
$$L=\frac{A}{N*π*D}$$
L:必要管長 [m]
A:伝熱面積(仮値) [m2]=254 m2
N:管本数=52
D:管外径 [m]=0.034 m
上式より、L=254/(52*π*0.034)≒46m
となりました。
流路数(パス数)の決定
以上の計算より、仮に1パスの熱交換器を想定すると、管本数:52本、管長:46mの熱交換器となりますが、現実にはそのような熱交換器は存在しません。
一般的に、管の製作、輸送の制約から管長の最大値は6m程度です。
仮に管長を6mとすると、管のパス数は46m/6≒7.67なので8パスの熱交換器となりますが、熱交換器の機械設計ではある程度のマージンが必要なので、ここでは30%のマージンをとって、46m*1.3/6≒10となり、計算上、管は10パスとなります。
ただし、熱交換器の管のパス数は伝熱効率の観点から、一基あたり6パス~8パスが上限となるので、今回は熱交換器の基数を増やし、6パスの熱交換器を2基設置することになります。
熱交換器の基数はシェルのパス数に等しいため、上記をまとめると、管長:6m、管のパス数:6パス、シェルのパス数:2パスと決定することができました。
シェル径、バッフル間隔の決定
シェル径の決定
1パスあたりの管本数は52本、流路数は6パスと決定されたため、今回設計する熱交換器の総本数は、
52*6=312本
となります。
今回はシェル側は冷却水で比較的汚れが少ないと仮定して、チューブ配列は三角ピッチで、チューブピッチは40mmとします。
チューブ配列やピッチの考え方はこちらの記事を参照ください。
また、シェル径は以下の計算で算出できます。
$$N=K_1\biggl(\frac{D_b}{D}\biggl)^{n}$$
$$D_b=D\biggl(\frac{N}{K_1}\biggl)^{1/n}$$
$$D_s=D_b+C$$
N:管本数
Db:バンドル径 [m]
D:管外径 [m]
Ds:シェル径 [m]
C:シェルのクリアランス [m]
K1:パス数に応じた係数
n:パス数に応じた係数
ここで、K1とnは熱交換器のチューブ配列とパス数によって定まる係数で、三角ピッチと四角ピッチでは以下の表の数字が使用されます。
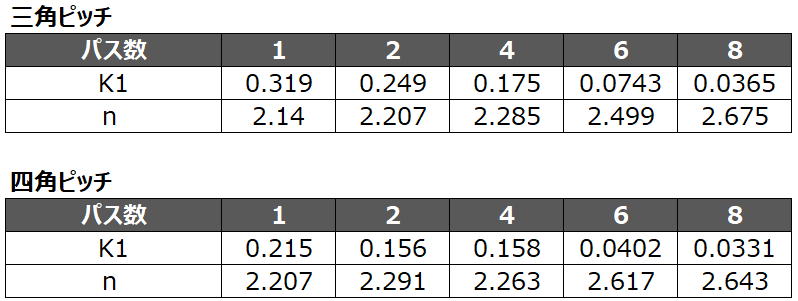
出典:Gavin P. Towler, R.K. Sinnott, Chemical Engineering Design, 5th ed., Amsterdam: Elsevier/Butterworth-Heinemann, 2008.
今回、三角ピッチでパス数は6なので、K1=0.0743、n=2.499を採用します。
上式に各条件を代入して計算すると、
Db=0.034*(312/0.0743)^(1/2.499)=0.958m
さらにシェルのクリアランスを0.05mと仮定してシェル径を計算すると
Ds=0.958+0.05=1.008m
と求めることができました。
バッフル間隔の決定
後の計算(シェル側の管外伝熱係数や圧力損失)に必要なので、ここでバッフル間隔を計算しておきます。
多管式熱交換器のシェル側(管外)はシェル、管を直角に横切る流れと考え、その流路面積はシェルを横切る管の隙間の合計とバッフル間隔の積となります。
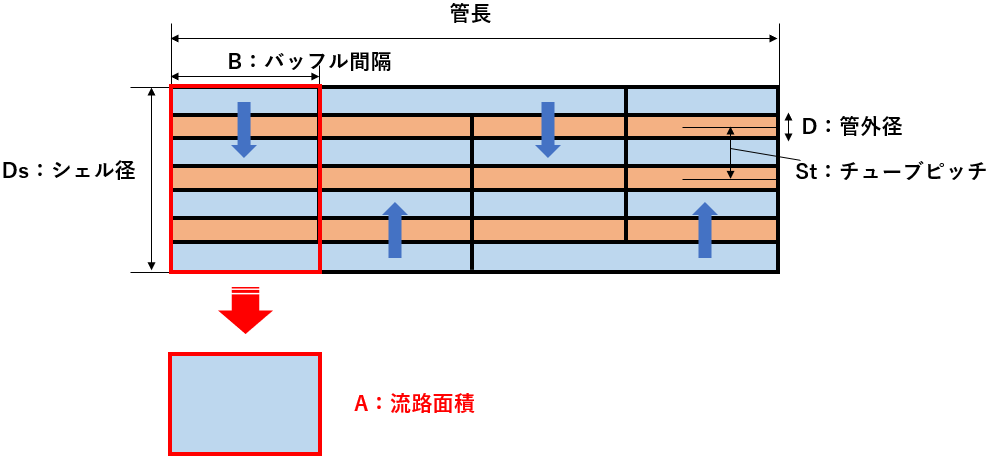
上図から、流路面積は赤枠の水色着色部分なので、全体から管の面積(オレンジ着色部)を差し引くことで算出できます。
$$A=D_sB-DB\frac{Ds}{S_t}$$
より
$$A=\frac{D_sB(S_t-D)}{St}$$
ここで、St-Dは伝熱管列の隙間なので、これをC'とすると、
$$A=\frac{D_sBC'}{St}$$
となります。
A:流路面積 [m2]
Ds:シェル径 [m]
B:バッフル間隔 [m]
D:管外径 [m]
St:チューブピッチ [m]
C':管列の隙間 [m]
また、シェル側の流速は1.0m/s程度を目安とするのが一般的なので、流速1.0m/sとなるような流路面積を計算すると、シェル側の流体(冷却水)の流量Fcは630 m3/hなので、
A=630/3600=0.175 m2
となります。
上記よりバッフル間隔Bは
$$B=\frac{AS_t}{D_sC'}$$
より
C'=0.04-0.034=0.006m
B=(0.175*0.04)/(1.008*0.006)=1.158m
と求めることができました。
また、この熱交換器の管長は6mとしているため、1シェルあたりのバッフル数は5枚となります。
伝熱係数の計算
管内伝熱係数の計算
管内伝熱係数の計算では、管内を乱流とみなし、コルバーンの式(Colburn's equation)を用いて算出します。
$$Nu=0.023Re^{0.8}Pr^{0.33}$$
$$Nu=\frac{h_1d}{k}$$
$$Re=\frac{ρud}{μ}$$
$$Pr=\frac{C_pμ}{k}$$
Nu:ヌセルト数
Re:レイノルズ数
Pr:プラントル数
d:管内径 [m]=0.027m
u:管内流速 [m/h]=1.5*3600 m/h
ρ:管内流体の密度 [kg/m3]=1090 kg/m3
μ:管内流体の粘度 [kcal/kg ℃]=4.32kcal/kg ℃
Cp:管内流体の比熱 [kcal/kg ℃]=0.9kcal/kg ℃
k:管内流体の熱伝導度 [kcal/m h ℃] = 0.54kcal/m h ℃
h1:管内伝熱係数: [kcal/m2 h ℃]
Nu=0.023*(1090*1.5*3600*0.027/4.32)^(0.8)*(0.9*4.32/0.54)^(0.33)=198.25
となるので、
管内伝熱係数h1は
h1=199.567*0.54/0.027=3965 kcal/m2 h ℃と求められました。
管外伝熱係数の計算
多管式熱交換器の管外伝熱係数は、シェル側にバッフルが設置されることにより流動が複雑になるため算出が難しく、様々な実験式が考案されています。
ここでは、簡易式であるコルバーンの式を用います。
※Re数が2000~32000の範囲で良く合うとされている。
<錯列配置>
$$Nu=0.33Re^{0.6}Pr^{0.33}$$
<直列配置>
$$Nu=0.8*0.33Re^{0.6}Pr^{0.33}$$
$$Nu=\frac{h_2D}{k}$$
$$Re=\frac{ρuD}{μ}$$
$$Pr=\frac{C_pμ}{k}$$
Nu:ヌセルト数
Re:レイノルズ数
Pr:プラントル数
D:管外径 [m]=0.034m
u:管外流速 [m/h]=1.0*3600 m/h
ρ:管外流体の密度 [kg/m3]=1000 kg/m3
μ:管外流体の粘度 [kcal/kg ℃]=3.67kcal/kg ℃
Cp:管外流体の比熱 [kcal/kg ℃]=1.0kcal/kg ℃
k:管外流体の熱伝導度 [kcal/m h ℃] = 0.5kcal/m h ℃
h2:管外伝熱係数: [kcal/m2 h ℃]
今回の例題では、三角ピッチの錯列配置なので、
$$Nu=0.33Re^{0.6}Pr^{0.33}$$
の式を用います。また、流体の物性は低温側(冷水)のものを使用します。
Nu=0.33*(1000*1.0*3600*0.034)^(0.6)*(1.0*3.67/0.5)^(0.33)=329.66
となるので、
管外伝熱係数h2は
h2=329.66*0.5/0.034=4848 kcal/m2 h ℃と求められました。
総括伝熱係数の計算
先ほどは熱交換器のパス数を決定するために、総括伝熱係数(U値)を750 kcal/m2 h ℃と仮決めしましたが、この項では求めた管内、管外の伝熱係数を元に正確な総括伝熱係数を計算します。
総括伝熱係数(管外基準)は以下の式で求めることができます。
$$U=\frac{1}{\frac{1}{h_2}+r_2+\frac{l_wD}{k_wd_m}+(r_1+\frac{1}{h_1})(\frac{D}{d})}$$
U:総括伝熱係数 [kcal/m2 h ℃]
h1:管内伝熱係数: [kcal/m2 h ℃]
h2:管外伝熱係数: [kcal/m2 h ℃]
r_1:汚れ係数(管内): [m2 h ℃/kcal]
r_2:汚れ係数(管内): [m2 h ℃/kcal]
d:管内径 [m] = 0.027m
D:管外径 [m] = 0.034m
dm:管平均径=(d+D)/2=0.0305 [m]
lm:管厚み [m]=(D-d)/2=0.0035 [m]
kw:管の熱伝導度 [kcal/m h ℃]
管内、管外の汚れ係数r1,r2はそれぞれ0.0002とします。
また、管の材質は炭素鋼とし、熱伝導度はkw=46 kcal/m h ℃とします。
それぞれの条件の上式に代入して、
U=1/(1/4848+0.0002+(0.0035*0.034)/(46*0.0305)+(0.0002+(1/3965)*(0.034/0.027))=943
となるので、総括伝熱係数(U値)は943 kcal/m2 h ℃と求めることができました。
前項で仮に決めたU値と比較すると、仮値は750 kcal/m2 h ℃だったので、十分余裕を持った設計になっていることが分かります。
注意:通常は計算で求めたU値は仮値を上回るように設計しますが、あまりに仮値より大きすぎると過剰設計になってしまうので、適切な余裕率(10%)となるように設計しなおすこともあります。
伝熱面積の決定
伝熱面積についても総括伝熱係数と同様に、先ほどはA=254m2と仮決めしていましたが、この項では熱交換器の形状から定まる補正係数を元に正確な伝熱面積を計算します。
補正係数を求めるには、まず高温、低温流体の入口、出口温度から「P」と「R」を計算します。
PとRは以下の式から計算されます。
$$P=\frac{T_{ho}-T_{hi}}{T_{ci}-T_{hi}}$$
$$R=\frac{T_{ci}-T_{co}}{T_{ho}-T_{hi}}$$
Thi:高温流体入口温度 [℃]=70℃
Tho:高温流体出口温度 [℃]=30℃
Tci:低温流体入口温度 [℃]=10℃
Tco:低温流体出口温度 [℃]=20℃
上記で計算したPとRから、設計する熱交換器のパス数に応じ平均温度補正係数Fを図から読み取ります。
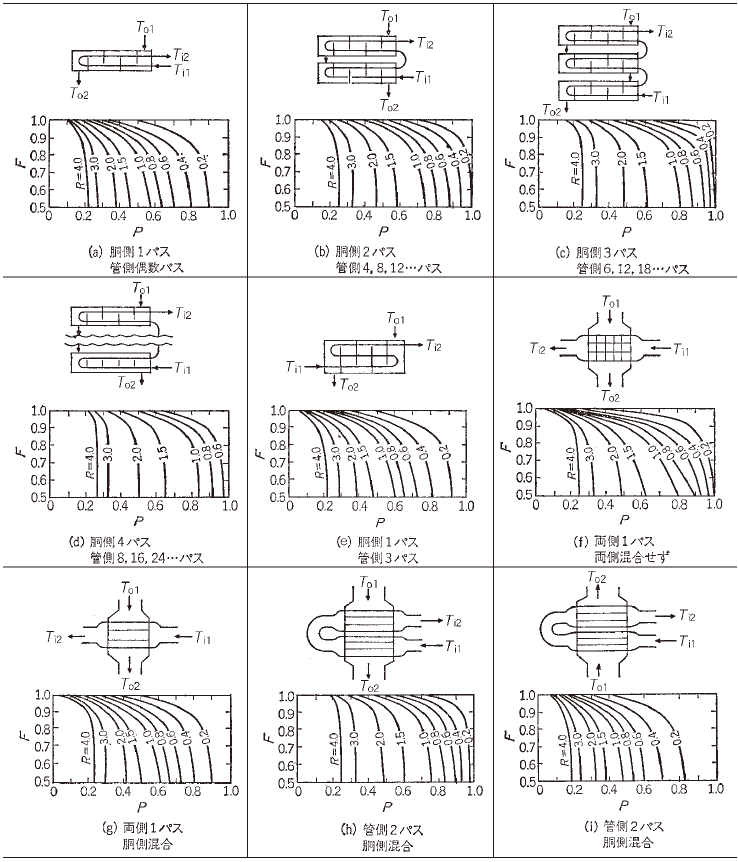
出典:化学工学便覧第6版
今回の流体温度からPとRを計算すると、
P=(30-70)/(10-70)=0.667
R=(10-20)/(30-70)=0.25
また、今回設計する熱交換器は菅側6パス、シェル側2パス(1パス×2基)であることを踏まえて図から読み取ると、
F=0.95
となります。
※R=0.25の線が無いので安全サイドでR=0.4の線から読み取り
注意:熱交換器の効率の面から、一般的にF>0.75が推奨されます。補正係数が0.75より下回る場合は設計の見直しが必要な場合があります。
対数平均温度差にこの補正係数を乗じると、
Tm'=Tm*F=33*0.95=31.4℃
となるので、前項で求めた総括伝熱係数Uから正確な伝熱面積を求めると、
A=6,278,400/(942*31.4)≒212m2
となります。
伝熱面積の仮値は254m2だったので、伝熱面積についても十分余裕を持った設計になっていることが分かります。
圧力損失の計算
管内圧力損失の計算
管内圧力損失は「摩擦による圧力損失」と「流路の曲がりによる圧力損失」を合計する必要があります。
それぞれの圧力損失は以下の式から求められます。
$$ΔP_t=ΔP_f+ΔP_r$$
$$ΔP_f=\frac{4fGt^2Lnn_s}{2gdρφ}*10^{-4}$$
$$f=0.046Re^{-0.2}$$
$$Gt=\frac{Fρ}{\pi/4d^2N}$$
$$ΔP_r=\frac{{3~4}Gt^2nn_s}{2gρ}*10^{-4}$$
ΔPt:菅側の合計圧力損失 [kg/cm2]
ΔPf:摩擦による圧力損失 [kg/cm2]
ΔPr:曲がりによる圧力損失 [kg/cm2]
f:管摩擦係数 [-]
Re:管内流体のレイノルズ数 [-]
Gt:1パスあたり質量速度 [kg/m2 h]
F:管内流体の堆積流量 [m3/h]=160 m3/h
L:管長 [m]=6m
n:パス数 [-]=6
ns:熱交換器の基数 [-]=2
d:管内径 [m]=0.027m
ρ:管内流体の密度 [kg/m3]=1090 kg/m3
g:重力加速度 [m/hr2]=9.8*3600^2 m/hr2
φ:粘度補正項 [-]=1.02(μ/μ_w)^0.14
μ:管内流体の粘度 [kcal/kg ℃]=4.32kcal/kg ℃
Gt=(160*109)/(π/4*0.027^2*52)=5.86*10^6 kg/h m2
f=0.046*(1090*1.5*3600*0.027/4.32)^(-0.2)=0.006
また、粘度補正項φのμwは、管壁の表面における粘度を意味します。
これを計算するには管壁の表面温度を計算する必要がありますが、簡易的な算出方法として「管内流体の平均温度」に「管内流体の平均温度と管外流体の平均温度の差の70%」を足した温度が用いられます。
今回の場合、管内流体の平均温度は(70+30)/2=50℃、管外流体の平均温度は(20+10)/2=15℃なので、管壁の表面温度は、50+0.7(50-15)=74.5℃となります。
よって、μwは74.5℃における粘度となり、上式に代入して粘度補正項を計算しますが、今回の計算例では簡単のため粘度補正項φ=1(粘度の温度依存性は無視)とします。
注意:温度変化の大きい熱交換器、粘度の温度依存性の大きい流体の場合は粘度補正項は無視せず計算するようにしてください。
まずは摩擦による圧力損失ΔPfを計算すると、
ΔPf=4*0.006*(5.86*10^6)^2*6*6*2/(2*9.8*3600^2*0.027*1090*1)*10^-4=0.74 kg/cm2
同様に流路の曲がりによる圧力損失ΔPrを計算すると
ΔPr=(3~4)*(5.86*10^6)^2*6*2/(2*9.8*3600^2*1090)*10^-4=0.45~0.6kg/cm2
従って、菅側の合計圧力損失ΔPtは、
ΔPt=0.74+(0.45~0.6)=1.19 ~ 1.34 kg/cm2と求められました。
補足:実際の熱交換器の設計では、熱交換器(特に菅側)の圧力損失がプロセス要求(許容圧力損失)を満足するかの確認が非常に重要となります。計算された圧力損失がプロセス要求を満足しない場合は、管の長さ、本数、パス数などの諸条件を変更して再度計算します。
シェル側圧力損失の計算
シェル側圧力損失は「管を横切るクロスフローの圧力損失」と「バッフルを超える場合の圧力損失」を合計する必要があります。
それぞれの圧力損失は以下の式から求められます。
$$ΔP_s=ΔP_c+ΔP_b$$
$$ΔP_c=\frac{4f{G_s}^2Ds(N+1)n}{2gρD_eφ}$$
$$ΔP_b=\frac{{G_b}^2Nn}{2gρC_o}$$
ΔPs:シェル側の合計圧力損失 [kg/cm2]
ΔPc:管を横切るクロスフローの圧力損失 [kg/cm2]
ΔPb:バッフルを超える場合の圧力損失 [kg/cm2]
f:管外摩擦係数 [-]
Gs:1パスあたり質量速度 [kg/m2 h]
Ds:シェル径 [m]
ρ:冷水密度 [kg/m3]
N:1シェル当たりのバッフル数
De:相当径 [m]
φ:粘度の補正項 [-]
Gb:切り欠き部の質量速度 [kg/m2 h]
Co:流出係数
同様に計算すると、ΔPc=0.285 kg/m3、ΔPb=0.155 kg/m3となるので、
シェル側の圧力損失ΔPsは、ΔPc+ΔPb=0.44 kg/m3と求めることができました。
ノズル径、構造の決定
ノズル径
今回、菅側の流量が160m3/h、シェル側の流量が630m3/hなので、ノズル径はそれぞれ6インチ、12インチとします。
補足:ノズル径は大きくしすぎると熱交換器の重量増加によるコスト悪化、小さくしすぎると圧力損失の増大の要因となるので、許容圧力損失を考慮しながら決定する必要があります。
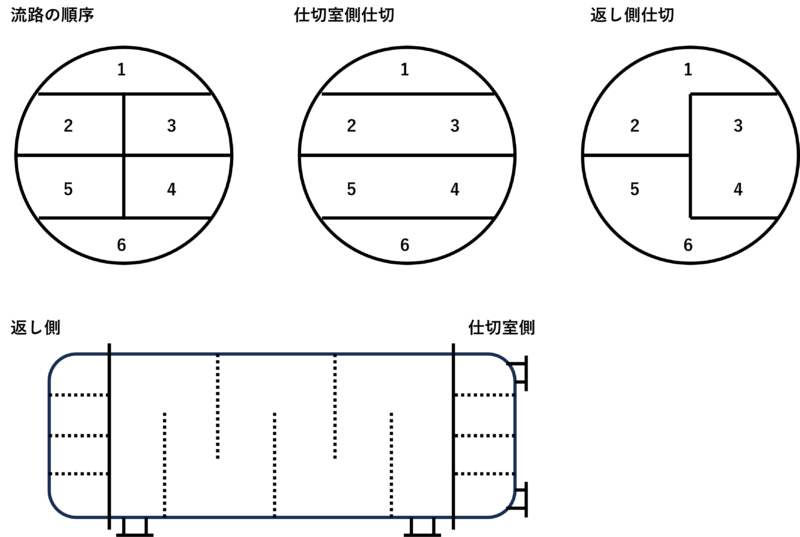
構造
今回の計算例では菅側の流路は6パス、バッフルは5枚なので、設計する熱交換器の構造の一例は以下の通りです。