今回の記事では横型タンク、横型ドラムの内容量の計算方法について解説します。
プラントでは、タンクやドラムに貯蔵されている液体の容量を直接測ることができないため、液面計の指示値をもとに、タンクテーブルを用いて容量を求めます。
タンクテーブルは、タンクの液レベル（液面の高さ）とその時の容量が一対一で記載されている表のことです。そのため、液レベルさえわかれば、タンクテーブルから読み取るだけで、液体の容量がわかります。
しかし、新設のタンクやドラムではタンクテーブルが無いため、自分で作成する必要があります。タンクテーブルを作成するためには、ある液面の高さにおける液体の容量を計算で求める必要があります。
計算サイトでは、タンクの径、長さ、液面の高さを入力すれば自動で容量が計算されるものがありますが、万が一計算が誤っている可能性もあるため、エンジニア自身が計算の中身を知っておくことは重要です。
そこで今回の記事では、タンクテーブルの作成に必要な、液面の高さから容量を求める方法について解説します。特に今回の記事では横型のタンク、ドラムにフォーカスして解説します。
縦型タンクについてはこちらの記事を参照下さい。
合わせて読みたい
・縦型タンクの内容量の計算方法、タンクテーブルの作成方法
・タンク、ベッセルの排水時間の計算方法の解説
・タンク,ドラムの液面計ノズル位置と滞留時間の決め方の解説
・プロセスエンジニアって何をする仕事？
・プラントエンジニアはブラックか？プラント設計概要と共に解説
・化学工学ってプラントエンジニアリングのどんな場面で使われる？
・化学メーカーとプラントエンジニアリング会社はどう違う？【就職・転職】
・海外出張って何を持っていけばいい？必携の持ち物、準備物を徹底解説
・【転職】（前編）化学メーカーからプラントエンジニアリング会社への転職で有利な点とは？
・【プラント設計基礎①】基本設計条項(Design Basis)
・【計装】プラントで使用される液面計(レベル計)の種類と特徴の解説
・【気液平衡】プラント設計で使用される気液平衡の推算モデルの解説
・プレコミッショニングとは？プラント試運転準備作業について解説
・【計装】差圧・圧力伝送器 (流量計、圧力計、レベル計) のトラブル事例と対策について
・【撹拌】Pv値とは？攪拌槽のスケールアップの留意点について解説
・【物性推算】沸点から蒸発熱、臨界温度を求める方法。「トルートンの規則」と「Guldbergの通則」について解説
・【物性推算】プロセスシミュレーションで使用される物性推算モデルの適用範囲の解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
・プラントで使用される保温材・断熱材の種類と特徴について解説
・保温材・断熱材はどんな基準で選定する？選定時の留意点について解説
・【配管】エロージョン速度とは？エロージョンを引き起こす配管流速について解説
・【配管】プラントで使用されるスプレーノズルの設計方法の解説
・プラントのプロセス制御性と最適な制御方式の考え方について解説
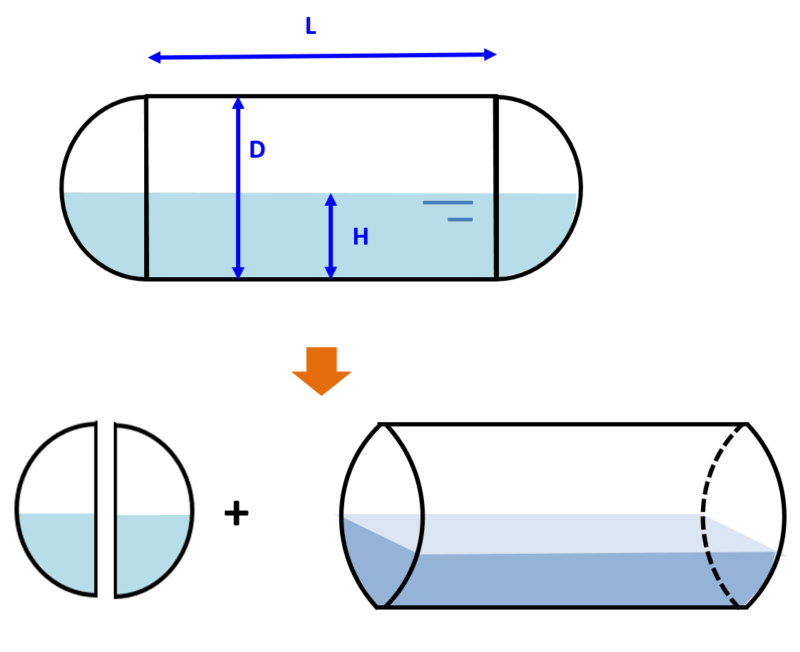
横型タンクモデル
上図のように、長さL、内径Dの横型タンクを考えます。また、鏡板は一般的な半楕円形の鏡であると仮定します。このタンクの高さがHの時の液の容量について考えます。
まずは、鏡板（左側）と銅（右側）に分割します。それぞれ形が異なるために、一つの式で表現することが出来ないためです。
そのため、鏡板と銅それぞれの容量を求める計算式を立て、それを足し合わせて全体の容量を算出する方針となります。
鏡板の容量
鏡板の容量の計算式は日本鏡板工業株式会社のカタログで公開されています。
鏡板の容量（片側）をVhとすると、計算式は以下の通りです。
$$V_h=\frac{π}{4}\biggl(\frac{D}{2}H^2-\frac{1}{3}H^3\biggl)$$
Vh：鏡板の容量（片側）
D：タンクの内径
H：液面の高さ
ただし、この計算式は片方の鏡板の容量なので、実際に横型タンクの容量を計算する際は2倍することを忘れないようにしてください。
そのため、鏡板の容量をV1とすると、計算式は以下の通りになります。
$$V_1=\frac{π}{2}\biggl(\frac{D}{2}H^2-\frac{1}{3}H^3\biggl)$$
V1：鏡板の容量
D：タンクの内径
H：液面の高さ
これで鏡板の体積V1が求まりました。
鏡板が半球の場合
鏡板が半球の場合は、分割した鏡板をあわせると、球形になることから、鏡板の容量を求めることは球冠の体積を求めることと同値です。
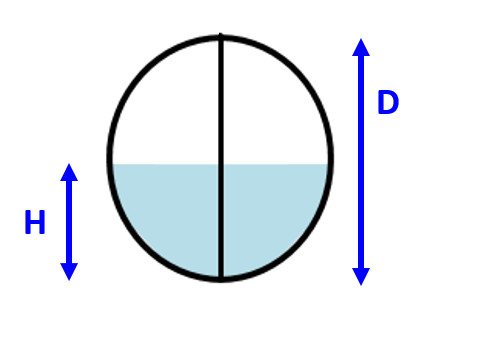
鏡板の容量を求める計算式は以下の通りです。
$$V_1=π\biggl(\frac{D}{2}H^2-\frac{1}{3}H^3\biggl)$$
V1：鏡板の容量
D：タンクの内径
H：液面の高さ
以上より、鏡板が半楕円場合、球の場合にそれぞれについて、鏡板の容量V1が求められました。
胴の容量
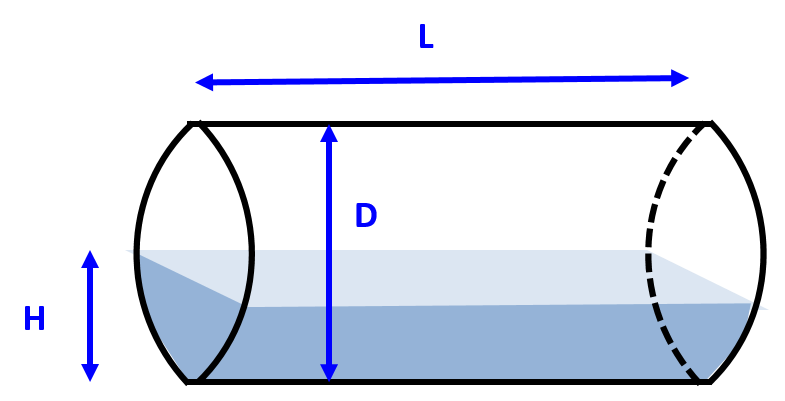
胴の容量を求めることは、横に倒した円柱の一部分の体積を求めることと同値です。
この体積は、円柱の体積同様、断面の面積に長さLを乗じることで求めることができます。
また、断面積は以下のように、扇形の面積から三角形の面積を引くことで求めることができます。
計算の前準備
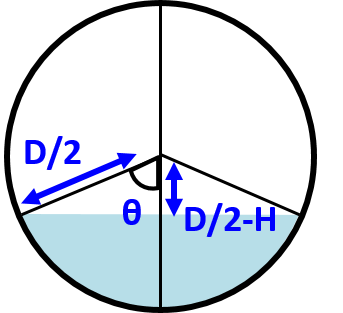
計算の前準備として、扇形をなす角のθを求めます。このθは断面積を求める時に使用します。
上図より、cosθを表すと
$$\cos{θ}=\frac{\frac{D}{2}-H}{\frac{D}{2}}=\frac{D-2H}{D}$$
となるので、逆関数で表すと、
$$θ=\cos^{-1}{\frac{D-2H}{D}}$$
θ：扇形をなす角
D：タンクの内径
H：液面の高さ
となります。
これでθが求まりました。
扇形の面積の計算
扇形の面積は円の面積に2θ/2πを乗じて求められますので、扇形の面積をS1と置くと、
$$S_1=\frac{π}{4}D^2\times\frac{2θ}{2π}$$
θを代入して整理すると、
$$S_1=\frac{D^2}{4}\cos^{-1}{\frac{D-2H}{D}}$$
S1：扇形の面積
D：タンクの内径
H：液面の高さ
となります。
これで扇形の面積S1が求まりました。
三角形の面積の計算
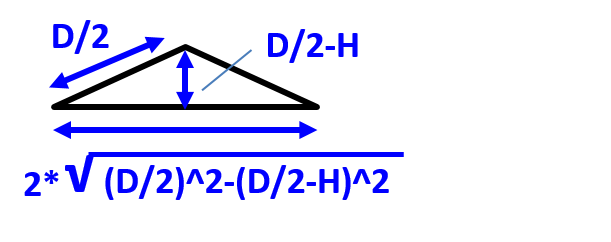
三角形の面積は底辺×高さ÷2で求められます。
三角形の底辺は三平方の定理から計算できます。
よって、三角形の面積をS2を置くと、
$$S_2=\biggl(\frac{D}{2}-H\biggl)\sqrt{\biggl(\frac{D}{2}\biggl)^2-\biggl(\frac{D}{2}-H\biggl)^2}$$
S2：三角形の面積
D：タンクの内径
H：液面の高さ
となります。
これで三角形の面積S2が求まりました。
胴の容量の計算
上述の通り、断面積は扇形の面積から三角形の面積を引くことで求められるので、断面積の面積をSと置くと、
※数式表示が途切れている場合はスライドすると表示されます。
$$S=S_1-S_2=\frac{D^2}{4}\cos^{-1}{\frac{D-2H}{D}}-\biggl(\frac{D}{2}-H\biggl)\sqrt{\biggl(\frac{D}{2}\biggl)^2-\biggl(\frac{D}{2}-H\biggl)^2}$$
となるので、胴の容量V2は断面積Sにタンクの長さLを乗じて、
V2：胴の液容量
S：断面積
D：タンクの内径
H：液面の高さ
L：タンク長さ
となります。
これで胴の容量が求まりました。
タンク容量の計算
タンク容量は鏡板の容量に胴の容量を足すことで求められるので、タンク容量をVとすると、
※数式表示が途切れている場合はスライドすると表示されます。
<鏡板が半楕円の場合>
<鏡板が半球の場合>
V1：鏡板の液容量
V2：胴の液容量
D：タンクの内径
H：液面の高さ
となります。
これでタンク内の液容量を求めることが出来ました。
まとめ
今回の記事では横型タンク、横型ドラムの内容量の計算方法について解説しました。
タンク、ドラムを新設する場合は自分でタンクテーブルを作成する必要がありますが、タンクテーブルを作成するためにはある液面の高さにおける液体の容量を計算で求める必要があります。
計算サイトでは、タンクの径、長さ、液面の高さを入力すれば自動で容量が計算されるものがありますが、万が一計算が誤っている可能性もあるため、エンジニア自身が計算の中身を知っておくことは重要です。
縦型タンクについてはこちらの記事を参照下さい。
今回の記事が参考になれば幸いです。ではまた他の記事でお会いしましょう。
