
今回の記事ではタンク、ベッセルの排水時間の計算方法について解説します。
プラントの定期修理(定修)などでシャットダウン操作を行う時は、タンク、ベッセル内の液抜きをする必要があります。また、プラント建設やプレコミッショニングで行う耐圧試験を水圧で行う場合は、試験終了後に水抜きをしなければなりません。
これらの操作での液抜き、水抜きではドレン弁を開けますが、タンクやベッセルの容量が大きいと液抜き、水抜き時間が想定外に長くなることもあり、シャットダウン工程、建設工事工程に影響を与える場合があります。
そんなとき、液抜き、水抜きに要する時間が事前に分かっていると、その後の工程を計画するのに便利です。
今回、ドレン弁の口径をオリフィスとみなしてタンク、ベッセルから液抜きをして空になるまでの時間を計算する方法について解説します。
合わせて読みたい
・プロセスエンジニアって何をする仕事?
・プラントエンジニアはブラックか?プラント設計概要と共に解説
・化学工学ってプラントエンジニアリングのどんな場面で使われる?
・化学メーカーとプラントエンジニアリング会社はどう違う?【就職・転職】
・【転職】(前編)化学メーカーからプラントエンジニアリング会社への転職で有利な点とは?
・横型タンクの内容量の計算方法の解説~タンクテーブルの作成~
・縦型タンクの内容量の計算方法、タンクテーブルの作成方法
・タンク,ドラムの液面計ノズル位置と滞留時間の決め方の解説
・【気液平衡】プラント設計で使用される気液平衡の推算モデルの解説
・プレコミッショニングとは?プラント試運転準備作業について解説
・耐圧試験圧力を設計圧力の1.5倍とするのは間違い?各規格の試験圧力を解説
・【配管】制限オリフィス孔径の計算手順の解説
・【配管】オリフィスの流量係数とは?形状との関係について解説
・【配管】液ラインの制限オリフィス孔径の簡易式とキャビテーション指数について
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】プラントで使用されるスプレーノズルの設計方法の解説
・【撹拌】Pv値とは?攪拌槽のスケールアップの留意点について解説
・【物性推算】沸点から蒸発熱、臨界温度を求める方法。「トルートンの規則」と「Guldbergの通則」について解説
・【物性推算】プロセスシミュレーションで使用される物性推算モデルの適用範囲の解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
・【蒸留塔】簡単に蒸留分離段数の目安を計算する方法の解説
・プラントで使用される保温材・断熱材の種類と特徴について解説
・保温材・断熱材はどんな基準で選定する?選定時の留意点について解説
・プラントのプロセス制御性と最適な制御方式の考え方について解説
・「濾過助剤」とは?プラントで使用される濾過助剤の種類と特徴について解説
計算モデル
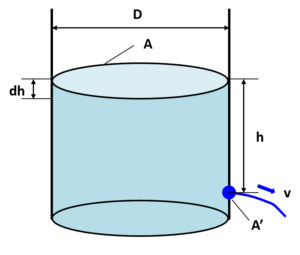
上図のように円筒形のタンクを考え、液面からh[m]下部にある穴から流速v[m/s]で液が流出しているとします。
微小時間dt[s]後、液面の高さはdh[m]減少しますので、以下の式が成り立ちます。
$$-dh・A=v・A'・dt$$
オリフィスの流量係数を考慮したトリチェリの定理より、
$$v=C_d\sqrt{2gh}$$
となるので、以下のように表せられます。
$$-dh・A=C_d\sqrt{2gh}・A'・dt$$
h:液面から孔までの距離 [m]
dh:微小時間dtで下がった液面 [m]
A:タンク液面の面積 [m2]
A':孔の面積 [m2]
dt:微小時間 [s]
Cd:流量係数
g:重力加速度 (g=9.81 [m/s2])
流量係数Cdはオリフィス形状によって異なる数字となりますが、概ねCd=0.61~1.0の値をとります。詳細についてこちらの記事で解説しています。
t=0でh=h1、t=tでh=h2を境界条件と上式を積分すると以下の通りになります。
※数式表示が途切れている場合はスライドすると表示されます。
$$t=-\int_{h_1}^{h_2}\frac{A}{C_dA'\sqrt{2gh}}$$
整理して、
タンクを空にする場合はh2=0なので、液抜き前の液面高さをh、タンク内径をD[m]とすると、液抜きに要する時間tは以下の通りになります。
<縦型円筒形タンクの液抜き時間>
$$t=\frac{2A}{C_dA'\sqrt{2g}}\sqrt{h}=\frac{πD^2\sqrt{h}}{2\sqrt{2g}C_dA'}$$
t:液抜きに要する時間[s]
h:液面の高さ
A:タンク液面の面積 [m2]
A':孔の面積 [m2]
Cd:流量係数
g:重力加速度 (g=9.81 [m/s2])
D:タンク内径[m]
これで円筒形のタンク、ベッセルの液抜きに要する時間を計算することができるようになりました。
他の形状については次項で解説していきます。
様々な形状のタンク、ベッセルの液抜き時間
横型円筒形タンク
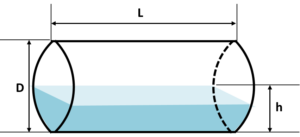
横型円筒形タンクの液抜きに要する時間は以下の式で表せられます。
<横型円筒形タンクの液抜き時間>
$$t=\frac{2\sqrt{2}L(D^{1.5}-[D-h]^{1.5})}{3C_dA'\sqrt{g}}$$
t:液抜きに要する時間[s]
h:液面の高さ
D:タンク内径[m]
L:タンク長さ[m]
A':孔の面積 [m2]
Cd:流量係数
g:重力加速度 (g=9.81 [m/s2])
球形タンク
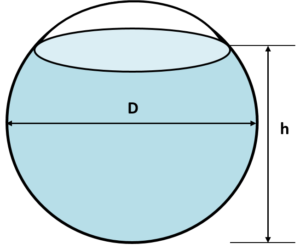
球形タンクの液抜きに要する時間は以下の式で表せられます。
<球形タンクの液抜き時間>
$$t=\frac{\sqrt{2}πh^{1.5}(D-0.6h)}{3C_dA'\sqrt{g}}$$
t:液抜きに要する時間[s]
h:液面の高さ
D:タンク内径[m]
A':孔の面積 [m2]
Cd:流量係数
g:重力加速度 (g=9.81 [m/s2])
下部コーン型タンク
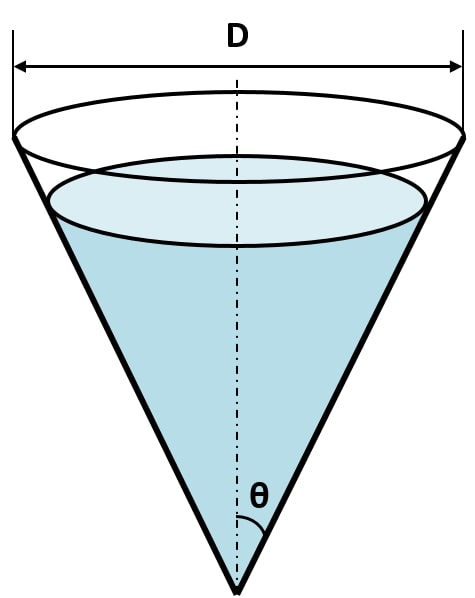
下部コーン型タンクの液抜きに要する時間は以下の式で表せられます。
<下部コーン型タンクの液抜き時間>
$$t=\frac{\sqrt{2}π(\tan{θ})^2Dh^{2.5}}{5C_dA'\sqrt{g}}$$
t:液抜きに要する時間[s]
h:液面の高さ
D:タンク内径[m]
θ:コーンをなす角[rad]
A':孔の面積 [m2]
Cd:流量係数
g:重力加速度 (g=9.81 [m/s2])
計算例
内径2mの球形タンクに1.6mの高さまで水が入っている場合、このタンクのドレン弁を開けて水抜きを行い、タンクが空になるまでの時間を計算します。
なおドレン弁の口径は2インチ(=50mm)とし、短管のフラット型オリフィスとみなします。
<球形タンクの液抜き時間>
$$t=\frac{\sqrt{2}πh^{1.5}(D-0.6h)}{3C_dA'\sqrt{g}}$$
Cd=0.8、A'=π/4×(0.05)^2=0.00196[m2]、D=2[m]、h=1.6を上式に代入すると、以下の通りになります。
$$t=\frac{\sqrt{2}π・1.6^{1.5}(2-0.6・1.6)}{3・0.8・0.00196\sqrt{9.81}}=1164$$
したがって、この条件の場合、液抜きに必要な時間は1164秒(=20分弱)ということになります。
まとめ
今回の記事ではタンク、ベッセルを空にするまでの時間の計算方法について解説しました。
プラントの定期修理(定修)などでシャットダウン操作を行う場合や、耐圧試験を水圧で行う場合は、液抜き・水抜き操作が必要となります。
液抜き、水抜きではドレン弁を開けますが、タンクやベッセルの容量が大きいと液抜き、水抜き時間が想定外に長くなることもあり、シャットダウン工程、建設工事工程に影響を与える場合があります。
そんなとき、液抜き、水抜きに要する時間が事前に分かっていると、その後の工程を計画するのに便利です。
この記事が役に立てば幸いです。ではまた他の記事でお会いしましょう。
