今回はオリフィスの流量係数及び形状との関係について解説します。
オリフィスの流量計算は、制限オリフィスの設計やオリフィス流量計の設計で行われますが、これらの計算には流量係数が登場します。
流量係数は定数ですが、文献値や設計前任者の数値をそのまま使用することが多く、オリフィスの計算では問題無いとしても、数字の根拠や使い分けについては不透明なことも多いです。
そこで、今回の記事ではオリフィスの流量係数の算出根拠とオリフィス形状による流量係数の使い分け方法について解説します。
合わせて読みたい
・【移動現象】粒子の抵抗係数と終端速度の計算方法の解説
・タンク、ベッセルの排水時間の計算方法の解説
・【配管】放熱/入熱による任意の地点における配管温度の導出
・【配管】家庭用水道管の凍結防止対策に対する定量評価
・【配管】放熱計算による配管が凍結するまでの時間の推定-伝熱モデルの解説-
・【配管】制限オリフィス孔径の計算手順の解説
・【配管】液ラインの制限オリフィス孔径の簡易式とキャビテーション指数について
・【配管】プラント配管の主な構成要素について解説
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】スパージャーの設計方法について解説
・【計装】 制御弁の開度、Cv値から流量を求める方法の解説
・【計装】差圧式流量計(オリフィス、フローノズル、ベンチュリ管)データシート作成方法の解説
・【計装】プラントで使用される流量計の種類と特徴の解説
・【計装】電磁流量計の設置上のポイントについて解説
・【計装】渦流量計の設置のポイントについて解説
・【計装】流量計のタイプ選定、設計時の留意点について解説
・プロセスエンジニアって何をする仕事?
・プラントエンジニアはブラックか?プラント設計概要と共に解説
・化学工学ってプラントエンジニアリングのどんな場面で使われる?
流量係数とは?
流量係数は流体の理論流速に対し、縮流による損失や摩擦による損失を考慮に入れて、実際の流速を表現するための補正係数です。
トリチェリの定理を用いて具体例を示します。
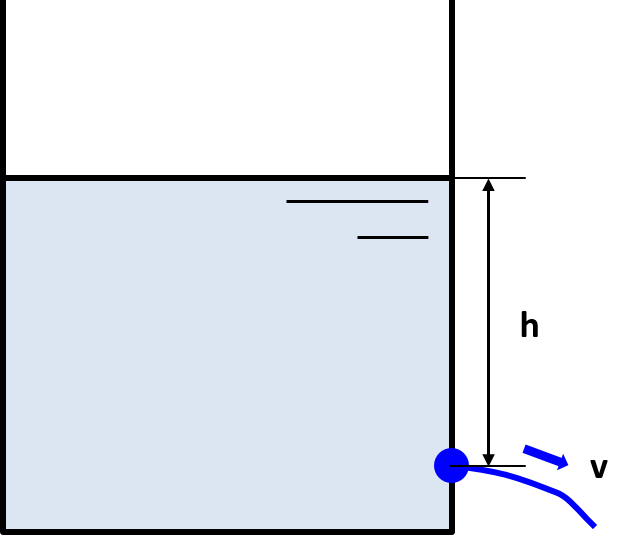
上図のような液体を貯蔵しているタンク(大気開放)を考え、液面からhの距離の孔から流出する液体の流速を考えます。
タンクの液面と孔についてのベルヌーイの定理が成り立つので、以下の等式が成り立ちます。
$$P+ρgh=P+\frac{1}{2}ρv^2$$
P:タンク液面と孔にかかる圧力(大気圧)
ρ:液密度
g:重力加速度
h:液面から孔までの距離
v:流速
これを整理して、流速vを求めると、以下の通りになります。これがトリチェリの定理です。
$$v=\sqrt{2gh}$$
しかし、この流速vはあくまでも理論値です。実際には孔の近傍における縮流による損失や摩擦による損失があるため、実流速は理論流速よりも小さい値になります。
そこで、この補正係数をCdとすると実流速は以下の通りになります。
$$v=C_d\sqrt{2gh}$$
この補正係数Cdが流量係数と呼ばれるものです。
さらにこの流量係数Cdは縮流による損失と摩擦よる損失を掛け合わせたものと考えると、それぞれ「収縮係数Ca」と「速度係数Cv」で表現すると以下の通りになります。
$$C_d=C_a\times{C_v}$$
Cd:流量係数
Ca:収縮係数(縮流による損失)
Cv:速度係数(摩擦による損失)
つまり、収縮係数Caと速度係数Cvが分かれば、流量係数Cdを計算することができます。
収縮係数Caはオリフィス孔の断面積と縮流部の断面積の比率ですが、オリフィスの形状によって縮流の状態が異なるため、縮流係数も異なる値となります。
一方、速度係数Cvは概ね0.96~0.98の値をとります。
次項から、それぞれのオリフィスの形状における収縮係数Ca及び流量係数Cdの計算方法について解説します。
シャープエッジオリフィス(Sharp Edged Orifice)
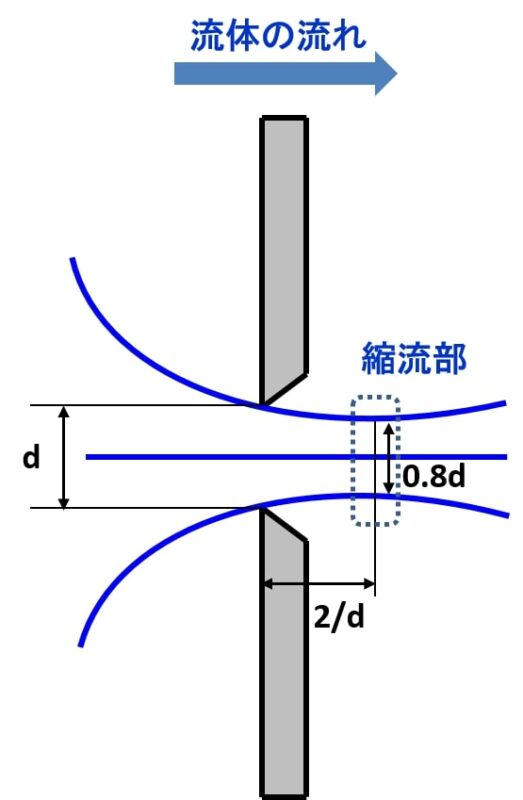
オリフィス流量計の流速測定部(オリフィス板)ではよく使用されるタイプです。
上図のように穴径dのオリフィスを通る流体は孔の出口近傍で縮流部(Vena contracta)を生じます。
上述のように、収縮係数Caはオリフィス孔の断面積と縮流部の断面積の比率であるため、それぞれにおける流速v、v'で表すと以下の通りになります。
$$C_a=\frac{v}{v'}$$
Ca:収縮係数
v:オリフィス孔における流速 [m/s]
v':縮流部における流速 [m/s]
また、オリフィスの穴径をd [m]とすると、シャープエッジオリフィスの場合、縮流部の径は0.8dになります。
さらに、オリフィス孔と縮流部それぞれの体積流量は等しいため、以下の等式が成り立ちます。
$$\frac{π}{4}d^2v=\frac{π}{4}(0.8d)^2v'$$
これを整理して
$$v=0.64v'$$
よって、収縮係数Caを計算すると、以下の通りになります。
$$C_a=\frac{v}{v'}=\frac{0.64v'}{v'}=0.64$$
これで、収縮係数Caを求めることができました。
次に流量係数Cdを計算します。
流量係数Cdは収縮係数Caと速度係数Cvをかけて計算されますが、速度係数Cvは上述の通り0.96~0.98を用います。よく使用される速度係数Cvは0.96です。
したがって、流量係数Cdを計算すると以下の通りになります。
$$C_d=C_a\times{C_v}=0.64\times0.96=0.61$$
Cd:流量係数
Ca:収縮係数(縮流による損失)
Cv:速度係数(摩擦による損失)
これでシャープエッジオリフィスの流量係数Cdは0.61と求めることが出来ました。
文献などでは唐突に流量係数=0.61と指定されることもありますが、この数値を成り立ちについて以上の通りです。
また、この数値の場合は液配管のオリフィス孔径の計算において簡易式を使用することが可能です。詳細はこちらの記事を参照ください。
フラット型オリフィス (Flat type Orifice)
フラット型オリフィスの流量係数の計算方法について解説します。
フラット型はストレート型とも言われますが、オリフィスの穴径とオリフィス板厚との関係による縮流部の発生状況が異なるので、場合分けで解説します。
板厚t≦d/8の場合
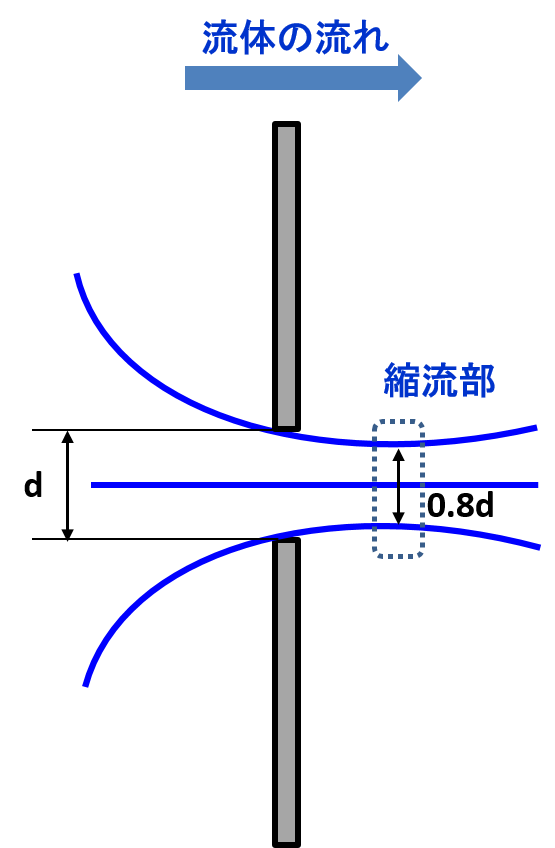
板厚tはオリフィス穴径dの1/8以下と、最も薄い板厚の場合です。
この時の縮流部の径は0.8dとシャープエッジオリフィスと同じです。故に収縮係数もシャープエッジオリフィスと同じとなるため、流量係数は以下の通りです。
板厚t≦d/8の場合
収縮係数Ca:0.64
速度係数Cv:0.96~0.98
流量係数Cd:0.61(Cv=0.96の場合)
d/8<板厚t<dの場合
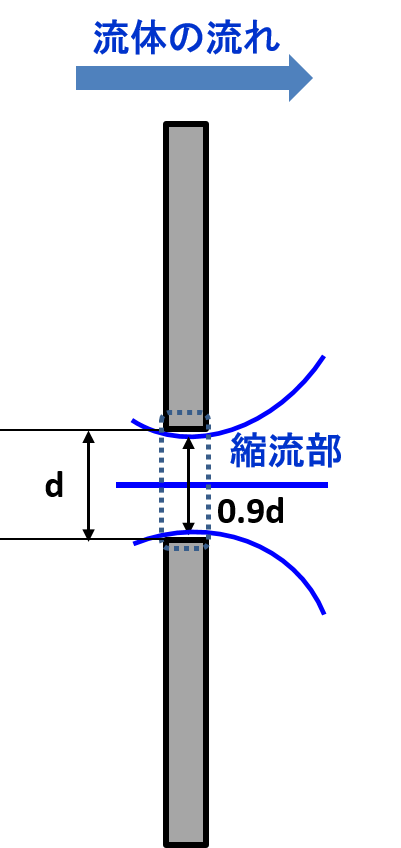
板厚tがd/8よりも大きく、dよりも小さい場合です。
この時の縮流部はオリフィス内部に発生し、この時の縮流部の径は0.9dです。
同様にして収縮係数を求めると、以下の通りです。
$$C_a=\frac{v}{v'}=\frac{(0.9)^2v'}{v'}=0.81$$
したがって、流量係数は以下の通りです。
d/8<板厚t<dの場合
収縮係数Ca:0.81
速度係数Cv:0.96~0.98
流量係数Cd:0.78~0.79
なお、実際の計算ではこの場合Cdの小数第二桁をまるめて流量係数Cd=0.8を代表値として使用することもあります。
板厚t≧dの場合
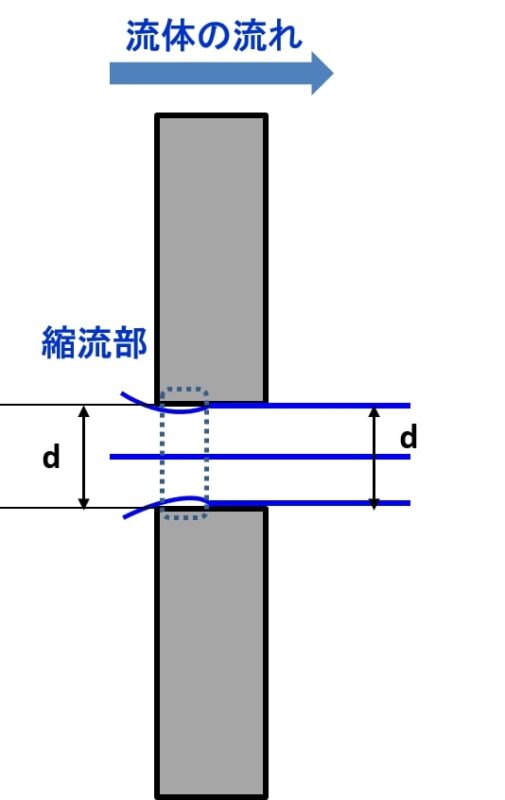
板厚tがオリフィス穴径dよりも大きい場合です。
この場合は縮流部はオリフィス内部にできるものの、オリフィス出口側における流体径は穴径と等しくなります。そのため、縮流部の径もオリフィス穴径と等しいとみなすことができます。
ゆえに、収縮係数Ca=1.0となります。
また、流量係数は以下の通りです。
板厚t≧dの場合
収縮係数Ca:1.0
速度係数Cv:0.96~0.98
流量係数Cd:0.96~0.98
なお、実際の計算では流量係数Cd=0.98を代表値として使用することもあります。
ラッパ型オリフィス(Trumpet-Shaped Orifice)
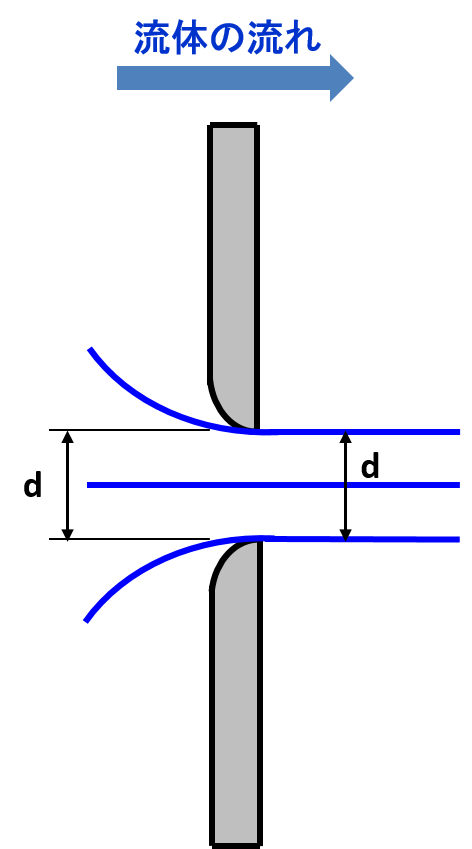
オリフィス孔がラッパ状の構造をもった場合です。
このタイプについては、縮流部が発生しないため、縮流部の径もオリフィス穴径と等しいとみなすことができます。
そのため、収縮係数Ca=1.0となります。
また、流量係数は以下の通りです。
ラッパ型オリフィスの場合
収縮係数Ca:1.0
速度係数Cv:0.96~0.98
流量係数Cd:0.96~0.98
このタイプも、実際の計算では流量係数Cd=0.98を代表値として使用することがあります。
まとめ
今回はオリフィスの流量係数及び形状との関係について解説しました。
オリフィスの流量計算は、制限オリフィスの設計やオリフィス流量計の設計で行われますが、これらの計算には流量係数が登場します。
流量係数は文献値の数字をそのまま使用することが多く、数字の根拠や使い分けについては不透明なことも多いですが、今回の記事を参考に制限オリフィスの計算、オリフィス流量計の設計に役立てば幸いです。

