今回は配管内に滞留した水が凍結するまでの時間を計算する方法について解説します。
前回は、流れがある場合における配管の伝熱モデルを作成し、保温有無による凍結リスクについて定量的に解説しました。
配管内部の水が0℃になったら凍結するという前提を置いておりました。
さらに、このモデルは定常状態を表現するモデルのため、時間項を考慮しておらず、水が滞留(流速=0m/s)の場合の凍結する時間は計算できませんでした。
今回、時間項を考慮した伝熱モデルを用いて、配管内に滞留した水が凍結するまでの時間の計算方法を解説します。
この計算はプラントにおける配管凍結防止の保温材(Winterization)の検討に使用されています。
自動計算ツールも提供されているようですが、プログラムの中身がブラックボックス化しているため、計算が誤っている可能性に気づけないことが問題です。
今回、伝熱モデル、及び計算方法について詳しく解説していきます。
プラントエンジニアであれば、モデルの内容を理解しておく必要があると思いますので、ぜひご一読下さい。
合わせて読みたい
・【配管】放熱/入熱による任意の地点における配管温度の導出
・【配管】家庭用水道管の凍結防止対策に対する定量評価
・【配管】プラントで使用される安全弁の種類と作動原理の解説
・【配管】プラントの音響疲労破壊とは?音響レベルの計算方法と対策
・【配管】プラント建設後の配管はどうやって洗浄する?配管洗浄方法の解説
・【配管】プラントの配管振動を引き起こす主な原因とその対策について
・【配管】プラントで使用されるストレーナーの種類と特徴の解説
・【配管】プラントで使用される減温器(デスーパーヒーター)の種類と特徴の解説
・【配管】プラント配管で使用されるエキスパンションジョイントの種類と特徴の解説
・【配管】制限オリフィス孔径の計算手順の解説
・【配管】オリフィスの流量係数とは?形状との関係について解説
・【配管】液ラインの制限オリフィス孔径の簡易式とキャビテーション指数について
・【配管】プラント配管の主な構成要素について解説
・【配管】プラントで使用されるスチームトラップの種類と特徴の解説
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】スパージャーの設計方法について解説
・【移動現象】粒子の抵抗係数と終端速度の計算方法の解説
・プラントで使用される保温材・断熱材の種類と特徴について解説
・保温材・断熱材はどんな基準で選定する?選定時の留意点について解説
伝熱モデル
伝熱モデルはJIS A9501 (2019)「保温保冷施工基準」のものを使用します。
計算式も原則JISに記載されている数式を使用します。
計算のステップは大きく3つに分かれます。
ステップ①:配管内の水の温度が0℃になるまでの時間を計算
ステップ②:0℃になった水が凍結するまでの時間を計算
ステップ③:ステップ①、②で計算した時間を合計する
この3つのステップで水が凍結する時間を求めることが可能
です。
ステップ① 配管内の水の温度が0℃になるまでの時間の計算
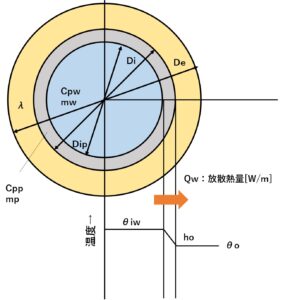
裸の配管と保温がある配管とでは、伝熱モデルが異なります。
それぞれのモデルについて詳しく解説していきます。
裸配管の伝熱モデル
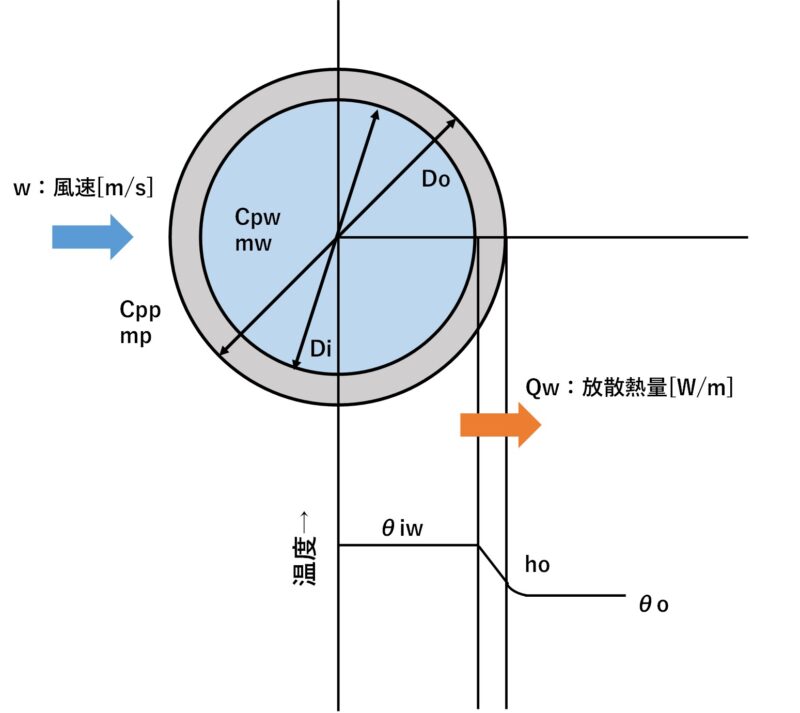
まず、管外伝熱係数hoを計算します。
hoの計算にあたり、強制対流と自然対流の2種類があります。
計算式は多くの実験式がありますが、JISが推奨しているのはそれぞれ以下の計算式で、比較的簡便に求められる計算式を推奨しているようです。
<自然対流>
Δθ≧10℃の場合
$$h_o = 2.56\timesΔθ^{0.25}$$
Δθ<10℃の場合
$$h_o = 3.61+0.094Δθ$$
水平配管の場合
$$h_o = 1.19\times(\frac{dθ}{D})$$
も使用可能
<強制対流>
Δθ≧10℃の場合
Δθ<10℃の場合
水平配管の場合
も使用可能
ho:配管外表面熱伝達係数 [W/m℃]
Δθ:温度差(θiw-θo) [℃]
θiw:初期温度 [℃]
θo:外気温度 [℃]
w:風速 [m/s]
D:配管外径[m]
配管の放熱計算では安全サイドをとって、厳しい方を採用します。
そのため、使用するhoは強制対流かつ、hoが最も大きくなる式を使用して下さい。
なお、JISでは
$$h_o = 2.56\timesΔθ^{0.25}\times(\frac{w+0.348}{0.348})^{0.5}$$
または
$$h_o =( 3.61+0.094Δθ)\times(\frac{w+0.348}{0.348})^{0.5}$$
のどちらかを使用することを推奨しています。
続いて放散熱量Qw[W/m]を計算します。
円管の外表面から放出されるQwは以下の式で計算できます。
$$Q_w=h_o\timesΔθ\timesπDo$$
Qw:放散熱量[W/m]
ho:配管外表面熱伝達係数 [W/m℃]
Δθ:温度差(θiw-θo) [℃]
θiw:初期温度 [℃]
θo:外気温度 [℃]
Do:配管外径[m]
したがって、JIS 9501 C.3式より、水が0℃になるまでの時間twp[h]は以下の式で計算できます。
なお、水は滞留しているため、個体とみなし、水の温度は一様に低下すると仮定しています。
そのため、管内基準の伝熱係数は未考慮です。
※数式の表示が途切れていたらスライドして表示させることが可能です。
twp:0℃になるまでの時間[h]
mw:管内の水の質量[kg]
mp:管の質量[kg]
Cpw:水の定圧比熱[kJ/kg℃] = 4.2[kJ/kg℃]
Cpp:管の定圧比熱[kJ/kg℃]
θiw:初期温度 [℃]
θice:凍結温度 [℃] = 0 [℃]
fs:配管断面積に対する安全率 JISでは75%以下を推奨
Qw:放散熱量[W/m]
l:配管長 [m]
ただし、
$$mw=\frac{π}{4}ρwlDi^2$$
$$mp=\frac{π}{4}ρpl(Do^2-Di^2)$$
mw:管内の水の質量[kg]
mp:管の質量[kg]
ρw:水の密度[kg/m3]
ρp:管の密度[kg/m3]
Di:内径[m]
Do:外径[m]
これで裸配管における、水が0℃になるまでの時間が計算ができるようになりました。
保温配管の伝熱モデル
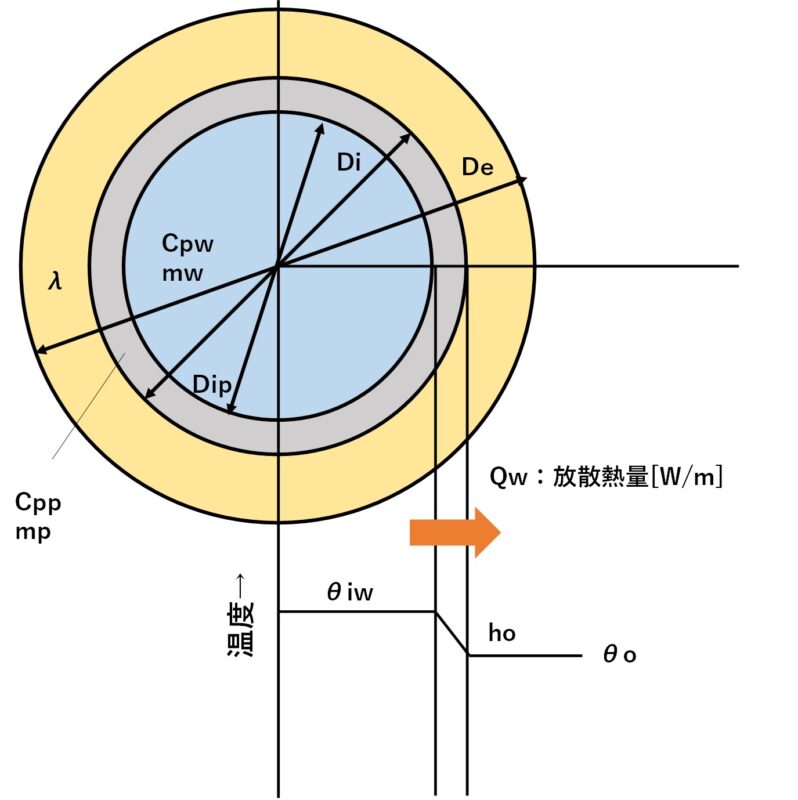
次は保温配管の場合の伝熱モデルを計算していきます。
裸配管との最大の違いは管外伝熱係数hoを考慮しないことです。
なぜなら、hoを考慮することは、管外(保温材の外表面)の熱抵抗を考慮することになり、放散熱量Qが小さく算出されてしまうことで、水が0℃になるまでの時間twpが大きく計算されてしまう(危険サイドの計算になる)ためです。
上述の通り、通常安全サイドで計算するため、保温がある場合の伝熱モデルでは外表面の伝熱係数は考慮せずに計算します。
逆に、裸配管で外表面の伝熱係数を考慮しない場合、算出されるtwpが小さくなりすぎて現実的ではない結果となってしまうため、上記の計算では伝熱係数を考慮しています。
このあたりの判断基準は理論よりも経験則に基づいており、実にプラントエンジニアリング的な思想だと思います。
まず、放散熱量Qwを計算します。
円管の外表面から放出されるQは以下の式で計算できます。
$$Q_w=\frac{(θiw-θo)\times2πλ}{\ln(De/Di)}$$
Qw:放散熱量[W/m]
λ:0℃における保温材の熱伝導率[W/℃ m]
θiw:初期温度 [℃]
θo:外気温度 [℃]
De:保温材外径[m]
Di:保温材内径[m]
したがって、JIS 9501 C.1式より、水が0℃になるまでの時間twp[h]は以下の式で計算できます。
保温有りの場合も、水は滞留しているため、個体とみなし、水の温度は一様に低下すると仮定しています。
そのため、管内基準の伝熱係数は未考慮です。
※数式の表示が途切れていたらスライドして表示させることが可能です。
twp:0℃になるまでの時間[h]
mw:管内の水の質量[kg]
mp:管の質量[kg]
Cpw:水の定圧比熱[kJ/kg℃] = 4.2[kJ/kg℃]
Cpp:管の定圧比熱[kJ/kg℃]
θiw:初期温度 [℃]
θice:凍結温度 [℃] = 0 [℃]
θo:外気温度 [℃]
fs:配管断面積に対する安全率 JISでは75%以下を推奨
Qw:放散熱量[W/m]
l:配管長 [m]
ただし、
$$mw=\frac{π}{4}ρwlDi^2$$
$$mp=\frac{π}{4}ρpl(Do^2-Di^2)$$
mw:管内の水の質量[kg]
mp:管の質量[kg]
ρw:水の密度[kg/m3]
ρp:管の密度[kg/m3]
Di:内径[m]
Do:外径[m]
これで保温配管における、水が0℃になるまでの時間が計算ができるようになりました。
ステップ②:0℃になった水が凍結するまでの時間の計算
ステップ②では裸配管も保温配管も同じ式で計算可能です。
まず、0℃になった水が凍結する際の放散熱量Qfを計算します。
$$Q_f=\frac{(-θo)\times{2πλ}}{\ln{(De/Di)}}$$
Qf:放散熱量[W/m]
λ:0℃における保温材の熱伝導率[W/℃ m]
θo:外気温度 [℃]
De:保温材外径[m]
Di:保温材内径[m]
したがって、JIS 9501 C.5式より、0℃になった水が凍結するまでの時間tfr[h]は以下の式で計算できます。
※数式の表示が途切れていたらスライドして表示させることが可能です。
tfr:0℃になった水凍結するまでの時間[h]
f:管内水の凍結割合 JISでは25%以下を推奨
fs:配管断面積に対する安全率 JISでは75%以下を推奨
Dip:配管内径[m]
hfr:水の凝固熱[kJ/kg] = 334 [kJ/kg]
Qf:放散熱量[W/m]
ρice:0℃における水の密度 [kg/m3] = 920 [kg/m3]
これで0℃になった水が凍結するまでの時間が計算ができるようになりました。
ステップ③:水が凍結するまでの時間の計算
ここまで来れば、後はステップ①で計算したtwpとステップ②で計算したtfrを合計するだけです。
$$t=t_{wp}+f_r$$
t:配管内に滞留した水が凍結するまでの時間[h]
twp:水が0℃になるまでの時間[h]
tfr:0℃になった水が凍結するまでの時間[h]
これで、配管内に滞留した水が0℃まで下がり、凍結する時間を計算することができました。
伝熱モデルの計算式を見てお気づきの方も多いと思いますが、安全率fsや凍結割合fの考え方次第でtが大きく変わってしまうことが分かります。
JISでは、fsは75%、fは25%を推奨していますが、プラント立地や会社の設計標準次第ではこの数値を調整した方が良いかもしれません。
まとめ
今回時間項を考慮した伝熱モデルを用いて、配管内に滞留した水が凍結するまでの時間の計算方法を解説しました。
計算にあたっては以下のステップで計算することが可能です。
ステップ①:配管内の水の温度が0℃になるまでの時間を計算
ステップ②:0℃になった水が凍結するまでの時間を計算
ステップ③:ステップ①、②で計算した時間を合計する
水、配管、保温材の物性値はほぼ固定値なので、凍結時間は実質、初期温度、外気温度、保温材厚み、安全率、凍結率だけ決まります。
実際の業務では、与えられた物性値、前提条件から保温材厚みを決めたり、保温材の適用可否(サイズが〇インチ以下であれば保温材を適用する)を決定します。
具体的には、プラント設計業務ではプロジェクトスペックにおける凍結防止対策に関する基準の作成業務に適用されます。
プロジェクトスペックに関してはこちらの記事を参照ください。
また、この計算自体はインターネット上のツールで手軽で計算できますが、中身がブラックボックス化しているので、計算の誤りに気付きにくいです。
もちろん、設計業務を効率化するために、このようなツール有効活用することは賛成ですが、プラントエンジニアとしては、計算の中身は一度は確認しておくべきと考えます。
今回の記事が役に立てば幸いです。ではまだ他の記事でお会いしましょう。


