【配管】放熱/入熱による任意の地点における配管温度の導出

今回は熱の入出熱(放熱/入熱)による任意の地点における配管温度の導出について解説します。

プラントにおける配管で流体を輸送する際、必ず熱の入出熱が発生し、熱損失(Heat Loss)が発生します。

通常は、配管に保温材やヒートトレース(蒸気トレースや電気トレース)を施工して熱損失を抑制します。

しかし、試運転時など、想定以上に放熱が大きく、配管温度が低下してしまい、予期せぬトラブルが発生してしまうことがあります。

管理人は、このようなトラブル対応として、熱損失の計算をすることがよくあるのですが、インターネット検索や文献では、目的に沿う例題、事例が見つかりませんでした。

そこで以下の通りの手順で、任意の配管長における流体温度を導出する式を作成しましたので、解説したいと思います。

化学工学、特に移動現象のエッセンスがちりばめられているので、教科書の復習としても最適です。

合わせて読みたい

伝熱モデルの定義

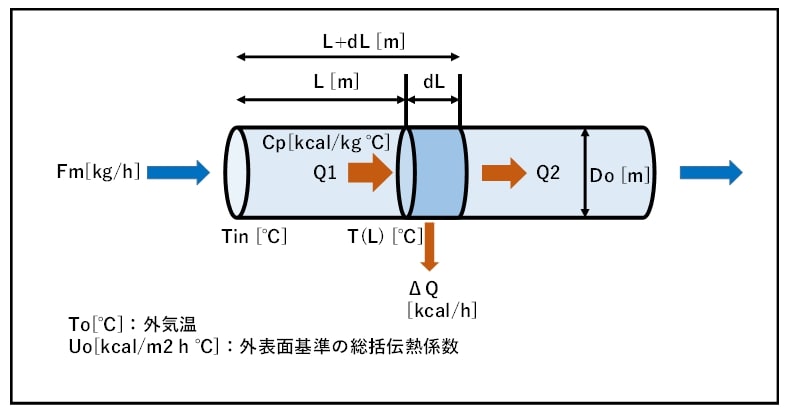
まず、上記のような配管の中の微小区間(長さdLの部分)における熱収支を考えます。

$$ΔQ = Q1-Q2$$

Q：熱量 [kcak/h]

Q1の熱量が微小区間に流入し、その区間の中でΔQの熱量が系外に流出、微小区間から流出される熱量はそれを差し引いた残りのQ2となります。

ここで、ΔQは微小区間の表面から放出される熱量なので、

$$ΔQ = Uo(πDodL)(T(L)-To)$$

Uo：外表面規準の総括伝熱係数 [kcal/m2 h ℃]
Do：外径 [m]
dL：微小区間の長さ [m]
T(L)：長さL[m]における温度[℃]
To：外気温[℃]

※微小区間ゆえに、配管温度T(L)は一定とみなしている

また、Q1-Q2は流体が微小区間で失った熱量なので、この区間の物質収支より、

$$Q1-Q2 = CpFmdT$$

Cp：流体の比熱[kcal/kg℃]
Fm：流体の質量流量[kg/h]
dT：微小区間の入/出における温度差[℃]

※流体の比熱は温度によらず一定とする。

ゆえに、

$$Uo(πDodL)(T(L)-To) = CpFmdT$$

と表すことができます。

上式を整理して、

$$\frac{dT}{(T(L)-To)} = αdL$$

ただし、

$$α = \frac{Uo(πDo)}{CpFm}$$

と置いた。

上記の微分方程式について、境界条件をL=0～L、T(L)=Tin~T(L)として積分すると、

$$\log\frac{T(L)-To}{Tin-To}=-αL$$

Tin：配管入口の温度[℃]

これを変形して

$$T(L)-To=(Tin-To)exp(-αL)$$

$$T(L) = To+(Tin-To)exp(-αL)$$

故に、αを算出すれば、任意の地点Lにおける温度T(L)を算出することが出来ます。

管内伝熱係数の算出

化学工学便覧第4版より、管内伝熱係数は以下の式で算出されます。

$$hi = \frac{0.0156CpG^{0.8}}{Di^{0.2}}$$

ただし、

$$G = \frac{Fm}{\frac{π}{4}Di^2}$$

hi：管内伝熱係数 [kcal/m2 h ℃]
G：単位面積あたりの質量流量 [kg/m2 h]
Cp：Cp：流体の比熱[kcal/kg℃]
Di：内径
Fm：流体の質量流量[kg/h]

管外伝熱係数の算出

管外のヌッセルト数を算出すると、化学工学第7版より、

※数式の表示が途切れていたらスライドさせると表示されます。

$$Nu = 0.3 +(\frac{ 0.62Re^{\frac{1}{2}}Pr^{\frac{1}{3}}}{{(1+(\frac{0.4}{Pr})^\frac{2}{3}})^{\frac{1}{4}}})( ({1+(\frac{Re}{282000})^\frac{5}{8}})^\frac{4}{5})$$

ただし、Re*Pr > 0.2が成り立つことを確認しておく。
管理人注)：ほとんどの場合、Re*Pr > 0.2となるので問題にはなりませんが、実際に計算する場合はこれが成り立つことを確認して下さい。

Re：レイノルズ数 [-]
Pr：プラントル数 [-]
※管外は大気なので、空気のプラント数が使用でき、化学工学便覧第7版より、Pr = 0.707が使用可能

ゆえに、管外基準の伝熱係数は、

$$ho = Nu\frac{λ}{Do}$$

ho：管外伝熱係数 [kcal/m2 h ℃]
λ：空気の熱伝導率 [W/m2 ℃]

総括伝熱係数Uoの算出

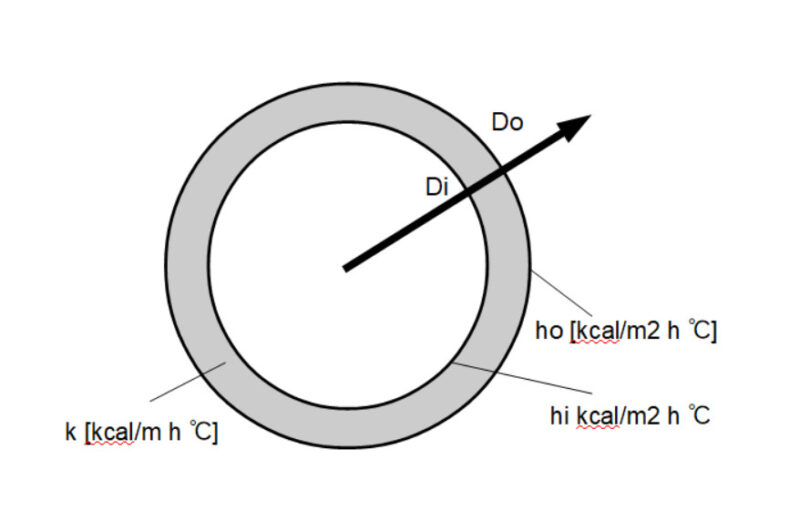
上記のような円筒の伝熱モデルを考えると、管外基準の総括伝熱係数Uoは以下の式で算出されます。

※数式の表示が途切れていたらスライドさせると表示されます。

$$Ｕo =\frac{1}{{(1/ho)+ri+(t/k)(Do/Dm)+(1/hi)(Do/Di)}}$$

Uo：管外基準の総括伝熱係数 [kcal/m2 h ℃]
ho：管外伝熱係数 [kcal/m2 h ℃]
hi：管内伝熱係数 [kcal/m2 h ℃]
ri：管内汚れ係数 [m2 h ℃/kcal]
t：配管厚み [m]
k : 配管熱伝導率 [kcal/m h ℃]
Di：内径 [m]
Do：外径 [m]
Dm：対数平均径 [m]