
今回の記事では制限オリフィスの孔径の計算手順について解説します。
制限オリフィス(restriction orifice)は高圧の流体を減圧する際、流量を調節したい場合に用いられ、制御弁と組み合わせて用いたり、コスト面から制御弁の代わりに用いることもあります。特にガスや蒸気の配管で多く用いられる傾向にあります。
本記事ではガス、蒸気配管における制限オリフィスの孔径の計算手順に焦点を当てて解説します。
液配管における制限オリフィス孔径の計算手順についてはこちらの記事を参照ください。
また、オリフィスの流量係数についてはこちらの記事を参照下さい。
計算手順は以下の通りです。
制限オリフィス孔径の計算手順
① 配管径、流量、圧力(減圧前、減圧後)を指定する。
② 配管流速 v [m/s]を計算する
③ 抵抗係数 Kを計算する。
④ 絞り直径比β(オリフィス孔径/配管径)を計算する。
⑤ オリフィス孔径を計算する。
制限オリフィスの孔径の計算手順は様々な方法がありますが、この計算手順は電卓のみ計算可能な方法です。
この計算手順において難しいのは③、④の手順です。次項からこれらの手順について詳細を解説します。
合わせて読みたい
・【配管】オリフィスの流量係数とは?形状との関係について解説
・【配管】液ラインの制限オリフィス孔径の簡易式とキャビテーション指数について
・【配管】放熱/入熱による任意の地点における配管温度の導出
・【配管】家庭用水道管の凍結防止対策に対する定量評価
・【配管】放熱計算による配管が凍結するまでの時間の推定-伝熱モデルの解説-
・【配管】プラントで使用される安全弁の種類と作動原理の解説
・【配管】プラントの音響疲労破壊とは?音響レベルの計算方法と対策
・【配管】プラント建設後の配管はどうやって洗浄する?配管洗浄方法の解説
・【配管】プラントの配管振動を引き起こす主な原因とその対策について
・【配管】プラントで使用されるストレーナーの種類と特徴の解説
・【配管】プラントで使用される減温器(デスーパーヒーター)の種類と特徴の解説
・【配管】マニュアルバルブ(手動弁)の選定基準について解説
・【配管】プラント配管で使用されるエキスパンションジョイントの種類と特徴の解説
・【配管】プラント配管の主な構成要素について解説
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】スパージャーの設計方法について解説
・【プラント設計基礎①】基本設計条項(Design Basis)
・【計装】どんな流量計が適切?流量計の種類の選定基準の解説
・【計装】プラントで使用される調節弁の種類と特徴の解説
・【計装】 制御弁の開度、Cv値から流量を求める方法の解説
・【計装】差圧式流量計(オリフィス、フローノズル、ベンチュリ管)データシート作成方法の解説
・【計装】調節弁データシート作成方法の解説
・【計装】プラントで使用される流量計の種類と特徴の解説
・【計装】プラントで使用される液面計(レベル計)の種類と特徴の解説
・【計装】プラントで使用される圧力計の種類と特徴の解説
・【計装】プラントで使用される温度計(温度センサ)の種類と特徴の解説
・【計装】プラントで使用される分析計の種類と特徴の解説
・【計装】差圧・圧力伝送器 (流量計、圧力計、レベル計) のトラブル事例と対策について
・【計装】電磁流量計の設置上のポイントについて解説
・【計装】渦流量計の設置のポイントについて解説
・【計装】流量計のタイプ選定、設計時の留意点について解説
・【移動現象】粒子の抵抗係数と終端速度の計算方法の解説
・タンク、ベッセルの排水時間の計算方法の解説
抵抗係数Kの計算
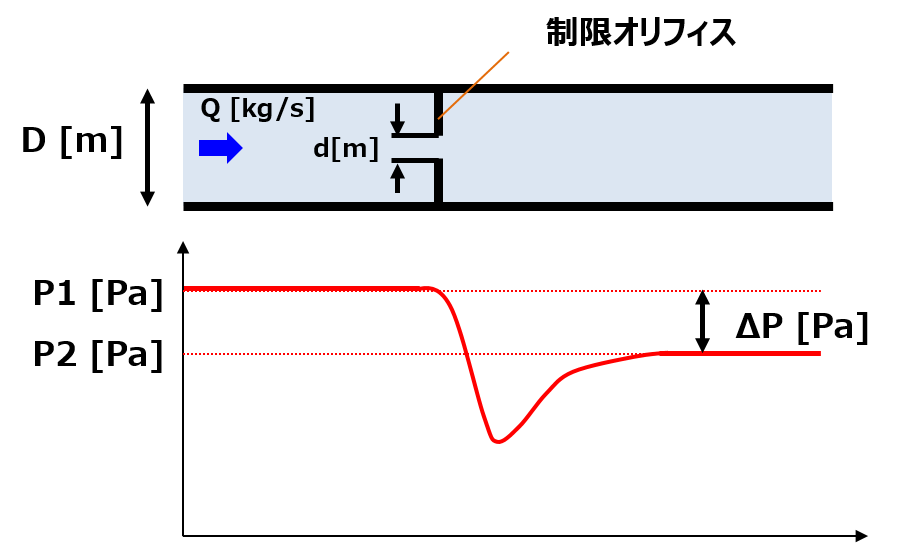
JIS Z 8762より、制限オリフィス前後の差圧ΔPと流量Qの関係式は以下の通りです。
$$Q=CYA_d\sqrt{\frac{2ρΔP}{1-β^4}}$$
Q:流量 [kg/s]
ΔP:差圧[Pa]
C:流出係数
Y:膨張係数
Ad:オリフィス孔面積 [m2]
ρ:上流側の流体密度 [kg/m3]
β:絞り直径比(オリフィス孔径 d [m] / 配管径 D [m]
ここで、
$$C_k=\frac{C}{\sqrt{1-β^4}}$$
とおいて整理すると、
$$ΔP=\frac{Q^2}{2ρY^2{A_d}^2}\frac{1}{{C_k}^2}$$
Q:流量 [kg/s]
ΔP:差圧[Pa]
Ck:流量係数
Y:膨張係数
Ad:オリフィス孔面積 [m2]
ρ:上流側の流体密度 [kg/m3]
β:絞り直径比(オリフィス孔径 d [m] / 配管径 D [m]
となります。
さらに流量Q[kg/s]を配管流速v [m/s]で表すと
$$Q=vAρ$$
さらに、
$$\frac{A_d}{A}=\frac{d^2}{D^2}=β^2$$
より、AをAdとβを使って表すと、
$$Q=vρ\frac{A_d}{β^2}$$
Q:流量 [kg/s]
v:配管流速 [m/s]
A:配管断面積 [m2]
Ad:オリフィス孔面積 [m2]
d:オリフィス孔径 [m]
D:配管径 [m]
ρ:上流側の流体密度 [kg/m3]
となります。これを上式に代入して、
$$ΔP=\frac{v^2ρ^2{A_d}^2}{β^4}\frac{1}{2ρY^2{A_d}^2}\frac{1}{{C_k}^2}$$
と表せられます。
$$K=\frac{1}{{C_k}^2Y^2β^4}$$
K:抵抗係数
と置いて約分すると
$$ΔP=\frac{1}{2}Kρv^2$$
変形して
$$K=\frac{2ΔP}{ρv^2}$$
となります。
これで、差圧、密度、配管流速から抵抗係数Kが計算できるようになりました。
絞り直径比βの計算
抵抗係数Kと絞り直径比βとの相関には以下のグラフのような関係成り立つことが知られています。
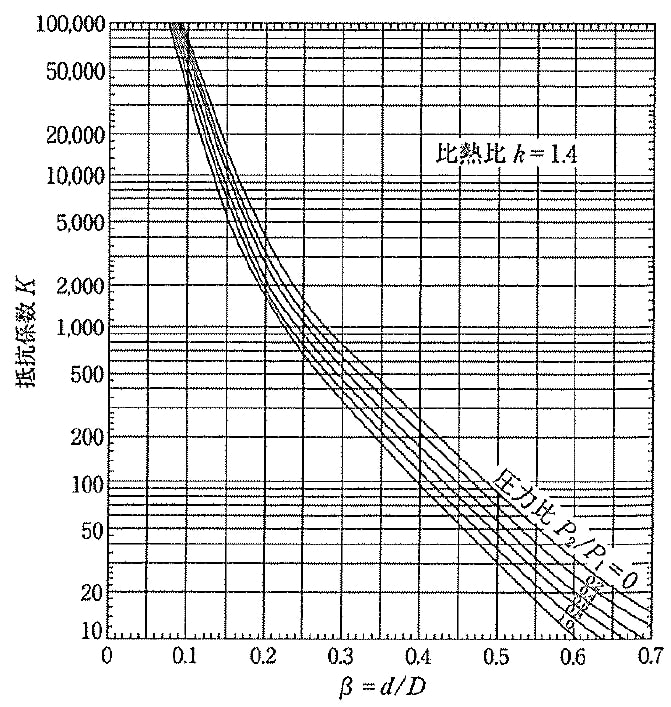
比熱比k=1.4の場合に成り立つ関係ですが、k=1.3でも概ね成り立つことが分かっており、通常使用するガスの比熱比k=1.3-1.4の範囲では適用可能です。
上記のグラフを数式で表すと以下の通りになります。
$$β=α_1{(\ln{K})}^2+α_2(\ln{K})+α_3$$
ただし
$$α_1=0.001322463t^2-0.00125t+0.006725$$
$$α_2=-0.025175422t^2+0.036595t-0.1649$$
$$α_3=0.119192281t^2-0.26158t+1.102177$$
t:圧力比 [P2/P1]
P1:オリフィス上流側圧力 [Pa]
P2:オリフィス下流側圧力 [Pa]
これで、抵抗係数Kから絞り直径比βが計算できるようになりました。
よって、オリフィス孔径dは
$$d=βD$$
D:配管径 [m]
の関係から配管径Dを用いることで計算されます。
計算例
ある蒸気配管を減圧する場合の制限オリフィス孔径を計算することを考えます。
前提条件は以下の通りとします。
前提条件
配管径D:6インチ(D=0.15m)
蒸気流量Q:1.5kg/s
密度ρ:2.5kg/m3
上流側圧力P1:450kPa
減圧後圧力P2:135kPa
まず、配管流速v [m/s]を計算すると、
$$v=\frac{Q}{ρA}=\frac{1.5}{2.5\times\frac{π}{4}\times0.15^2}=34$$
となります。
$$ΔP=P_1-P_2=315\times10^3$$
より、抵抗係数Kを計算すると、
$$K=\frac{2ΔP}{ρv^2}=\frac{2\times315\times10^3}{2.5\times34^2}=218$$
となります。
さらに、圧力比tは
$$t=\frac{P_2}{P_1}=0.3$$
なので、絞り直径比βを計算すると、
$$β=α_1{(\ln{218})}^2+α_2(\ln{218})+α_3=0.381$$
となります。
したがって、オリフィス孔径dは
$$d=βD=0.318\times0.15=0.057$$
より0.057mと求めることが出来ました。
まとめ
今回の記事では制限オリフィスの孔径の計算手順について解説しました。
制限オリフィスの孔径は以下の手順で求められます。
制限オリフィス孔径の計算手順
① 配管径、流量、圧力(減圧前、減圧後)を指定する。
② 配管流速 v [m/s]を計算する
③ 抵抗係数 Kを計算する。
④ 絞り直径比β(オリフィス孔径/配管径)を計算する。
⑤ オリフィス孔径を計算する。
この記事が参考になれば幸いです。ではまた他の記事でお会いしましょう。

