今回の記事では、プラント設計で使用される気液平衡の推算モデルについて解説します。
プラント設計におけるプロセスエンジニアの業務のとして、
・プロセスデータシート作成
・PFD、マテリアルバランス作成
などがありますが、データシート作成においては、対象となるプロセス流体の移動物性、熱物性が必要となります。純物質や単純な混合物であれば文献値を使用すれば良いですが、実際のプラントは多種多様な混合物を扱うので、単純に文献値を用いることができません。
また、PFDやマテリアルバランスを作成するためには、プラントの各機器における物質や熱の挙動を正確に計算、予測(特に気液平衡の計算)をしなければなりません。こちらも同様の理由で文献値を使えず、簡単に計算することが出来ません。
これらを解決するために、プロセスエンジニアの必須のツールがプロセスシミュレーターです。プロセスシミュレーターでは気液平衡の推算モデルを選択しなければ計算が出来ませんが、どの推算モデルを使用するかで計算結果が大きく変わってしまいます。
補足:プロセスシミュレーターはプラントの各プロセスで物質移動、熱移動、化学反応などの単位操作をコンピュータ上で計算するためのツールです。有名なものだとAspen+(AspenTech社)やPROII(AVEVA社)などがありますが、詳細は別記事にて解説したいと思います。
補足:固体を扱うプラントでは、固液平衡も考慮する必要がありますが、基本的な考え方は気液平衡と同じなので、本記事では概念を簡単に説明するために、気液平衡に焦点を当てて解説しています。また、二液相となる気液液平衡についても同様です。
気液平衡の推算モデルは大きく分けると以下の2つに分けられます。
主な推算モデル
① 活量係数モデル
② 状態方程式モデル
そこで、本記事では、これらの気液平衡の推算モデルについて、成り立ちと使い分けについて解説していきます。
気液平衡に代表される、プラントの相平衡の理解はプロセスエンジニアとしては必須事項です。これを理解しておかないと、シミュレーションによる計算結果の吟味が出来なくなるため、誤った計算を結果を正としまう可能性があります。プラント全体の設計(機器設計、配管設計、計装設計)に大きく影響しますので、是非ご一読下さい。
また、本記事で紹介した推算モデルを含めた各推算モデルの適用範囲についてはこちらの記事で紹介しています。
合わせて読みたい
・プロセスエンジニアって何をする仕事?
・プラントエンジニアはブラックか?プラント設計概要と共に解説
・化学工学ってプラントエンジニアリングのどんな場面で使われる?
・化学メーカーとプラントエンジニアリング会社はどう違う?【就職・転職】
・【プラント設計基礎①】基本設計条項(Design Basis)
・【プラント設計基礎③】プロセスフロー図(PFD)、マテリアルバランス
・水素は減圧すると温度が上昇する?知っておくべき圧縮水素の物性について解説
・横型タンクの内容量の計算方法の解説~タンクテーブルの作成~
・縦型タンクの内容量の計算方法、タンクテーブルの作成方法
・タンク、ベッセルの排水時間の計算方法の解説
・タンク,ドラムの液面計ノズル位置と滞留時間の決め方の解説
・【計装】調節弁データシート作成方法の解説
・【蒸留塔】棚段塔・充填塔の設計手順、データシート作成方法の解説
・【蒸留塔】簡単に蒸留分離段数の目安を計算する方法の解説
・【回転機】真空ポンプの排気時間の計算方法の解説
・【撹拌】Pv値とは?攪拌槽のスケールアップの留意点について解説
・【物性推算】沸点から蒸発熱、臨界温度を求める方法。「トルートンの規則」と「Guldbergの通則」について解説
・【物性推算】プロセスシミュレーションで使用される物性推算モデルの適用範囲の解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
・【熱交換器】多管式熱交換器(シェル&チューブ式)の流速、レイノルズ数の計算方法について解説
・【吸収塔】吸収塔高さの計算に必要な移動単位数(NTU)を図解法で求める方法の解説
・サットンの式とは?毒性ガス、可燃性ガスの着地濃度の計算方法について解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
理想状態の気液平衡
まずは、理想状態の気液平衡について考えます。
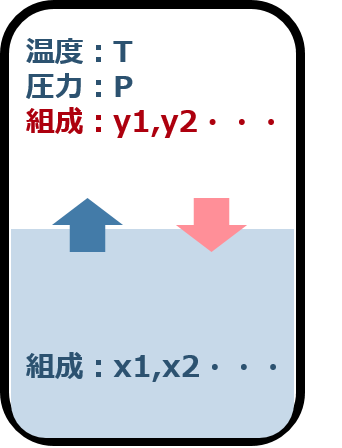
理想状態の気液平衡ではRault式(ラウール式)が成り立ちます。
例えば、大気圧下のベンゼン-トルエン系の気液平衡は理想状態とみなされます。
<Rault式>
$$P*y_i = P_{si}*x_i$$
P:全圧
Psi:成分iの飽和蒸気圧
xi:成分iのモル分率
yi:成分iのモル分率
式の意味を解説しておくと、右辺は全圧に気相成分のモル分率をかけているので、気相の分圧を表しています(ドルトンの法則)。言い方を変えると、気相中の成分iが液相を押さえつけようとしている力のようなイメージです。
右辺は成分iの飽和蒸気圧に成分iの液相組成をかけたものです。飽和蒸気圧はその成分が蒸発する温度で生じる圧力なので、右辺の言い方を変えると、液相中の成分iが気相を押し上げようとしている力のイメージです。
そのため、左辺=右辺となる時は、成分iについて、液相を抑えつける力と気相を押し上げようとする力が釣り合っており、、これはまさしく気液平衡になっている、と解釈することが出来ます。
また、成分iの飽和蒸気圧は、Antoine式(アントワン式)で温度の関数として表すことが出来ます。
<Antoine式>
$$P_{si}=\exp\biggl(A-\frac{B}{C+T}\biggl)$$
Psi:成分iの飽和蒸気圧
T:温度
A,B,C:成分iのAntoine定数
Antoine定数は化学工学便覧等の文献に載っていますので、それを使用します。これで温度が分かれば、その物質の飽和蒸気圧を求めることができます。
注意:Antoine定数を使用する時は、必ず式の形と単位に気を付けて下さい。文献によってAntoine式の形(指数で表現されているか対数で表現されているか)や、温度の単位(℃かKか)が異なります。
上記のRault式とAntoine式を使うことで、温度と全圧が分かれば、液相から気相の濃度、気相から液相の濃度を求めることが出来ます。
これらの関係をグラフで表すと以下の通りになります。
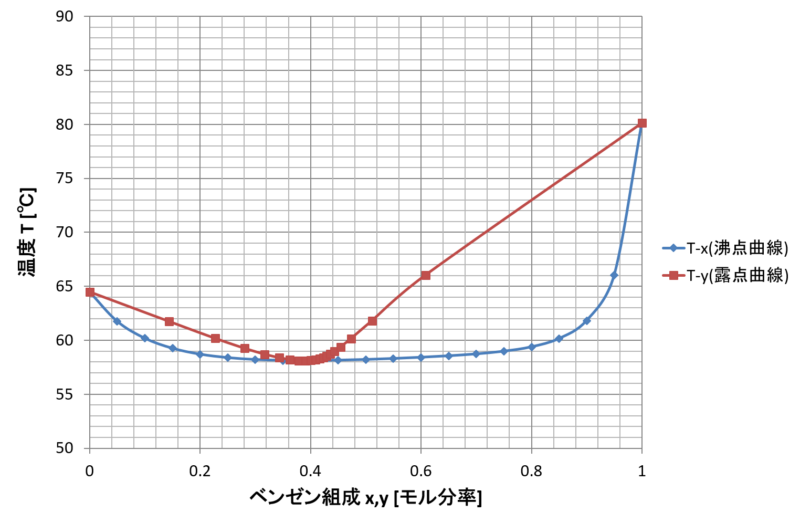
■ベンゼン-トルエン2成分系の大気圧下におけるT-xy線図
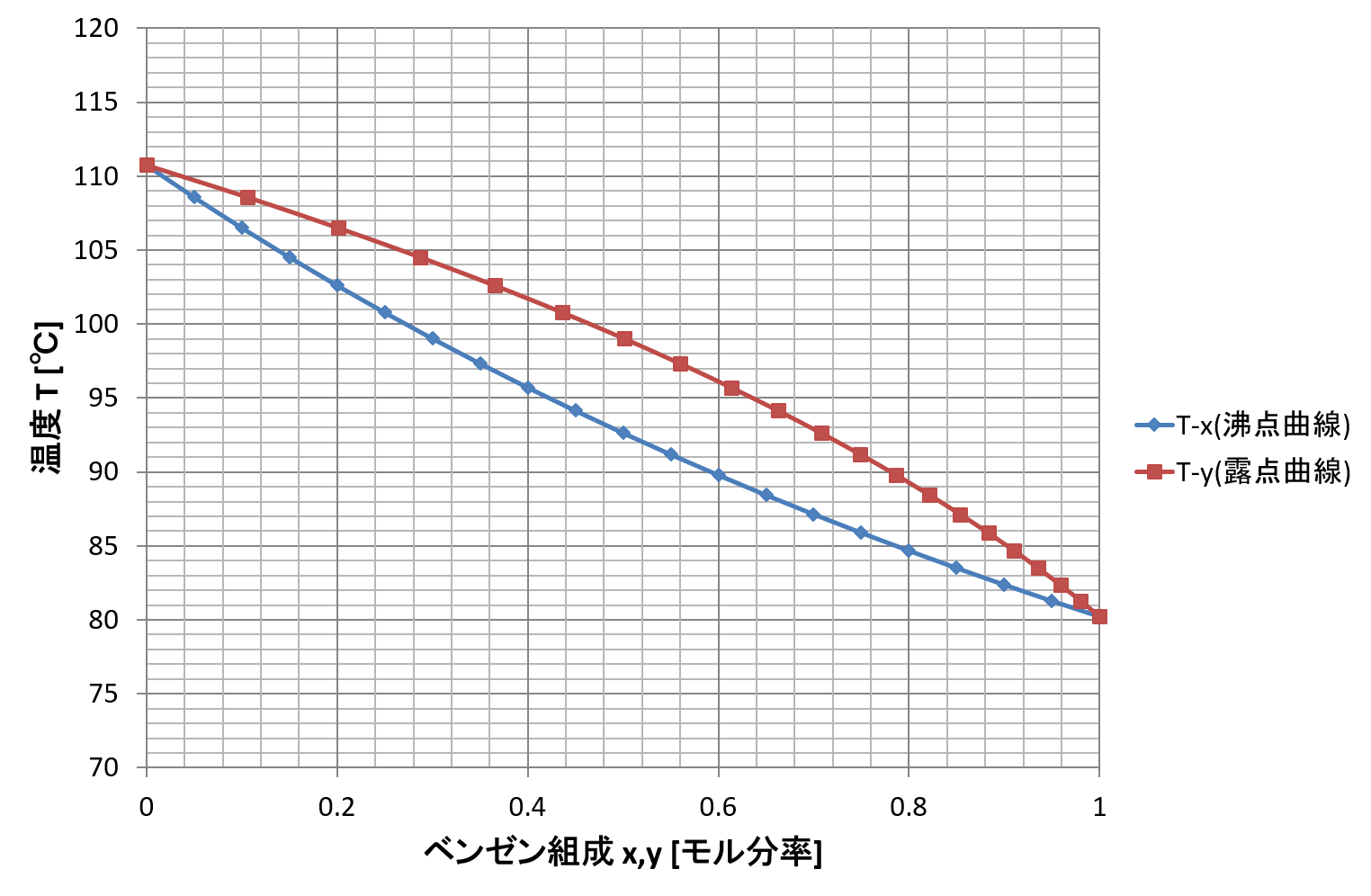
気液平衡状態では、沸点曲線上で液相の組成、露天曲線上で気相の組成を表します。
例えば、温度が90℃で、液相中のベンゼンのモル分率が0.6(60mol%)の場合、沸点曲線上の(0.6, 90)の点から右に直線を引いて露点曲線と交わった所が気相中のベンゼンのモル分率となります。グラフを読み取ると、およそ0.78(78mol%)となることがわかります。
ここまで、理想状態における気液平衡について解説しました。しかし理想状態とみなせるのは、常圧かつベンゼン-トルエン系のように分子同士の相互作用を無視しても良い場合(極性が無い場合)に限られます。
実際のプラントで取り扱う物質は極性を持つ成分だったり、高圧の系となることがほとんどです。極性を持つ物質や高圧の系では、上述した理想状態から大きく異なる気液平衡状態となるので、それをうまく表現してやるアプローチが必要となります。
先人達の尽力の結果生まれたアプローチが活量係数モデルと状態方程式モデルです。
活量係数モデル
まずは活量係数モデルについて解説します。
活量係数モデルはRault式の液相側に非理想性を補正する項(活量係数)を導入したモデルです。
<活量係数モデル>
$$P*y_i = γ_i*P_{si}*x_i$$
P:全圧
Psi:成分iの飽和蒸気圧
xi:成分iのモル分率
yi:成分iのモル分率
γi:活量係数
この活量係数には成分nと成分n+1の相互作用パラメータを含んでおり、実験値に合うようにパラメータの決定に工夫が凝らされ、活量係数モデルも様々なものが考案されています。
代表的なモデルでプラント設計業務でもよく用いられているのが、NRTLモデル(NRTL式)やWilsonモデル(Wilson式)です。
それぞれの活量係数パラメータを参考までに下記に記載します。大まかには「推算しようとしている流体のある二成分の相互作用を表すパラメータが考慮されている」と理解しておけば問題ありません。
<NRTLモデル>
NRTLはNon Random Two-Liquidの略称です。
※数式表示が途切れている場合はスライドすると表示されます。
ただし
$$G_{12}=\exp{(-α_{12}τ_{12})}$$
$$G_{21}=\exp{(-α_{12}τ_{21})}$$
$$τ_{12}=\frac{(g_{12}-g_{22})}{RT}$$
$$τ_{21}=\frac{(g_{12}-g_{11})}{RT}$$
x1:成分1の液相モル分率
x2:成分2の液相モル分率
(g12-g11):NRTLパラメータ
(g12-g22):NRTLパラメータ
α12:NRTLパラメータ(α12=0.2~0.47)
<Wilsonモデル>
ただし
$$Λ_{12}=\frac{V{_{m,2}}^L}{V{_{m,1}}^L}\exp{\biggl[-\frac{(λ_{12}-λ_{11})}{RT}\biggl]}$$
$$Λ_{21}=\frac{V{_{m,1}}^L}{V{_{m,2}}^L}\exp{\biggl[-\frac{(λ_{12}-λ_{22})}{RT}\biggl]}$$
x1:成分1の液相モル分率
x2:成分2の液相モル分率
(λ12-λ11):Wilsonパラメータ
(λ12-g22):Wilsonパラメータ
Vm1L:成分1の液相モル容積
Vm2L:成分2の液相モル容積
非理想性を示す系の典型例としてはベンゼン-メタノールの二成分系です。メタノールは典型的な極性物質なので、Rault式が成り立ちません。
下記に示したのが、理想状態とみなして描いたT-xy線図(上段)で、NRTLモデルで描いたT-xy線図(下段)です。
■理想状態とみなしたベンゼン-メタノール2成分系の大気圧下におけるT-xy線図
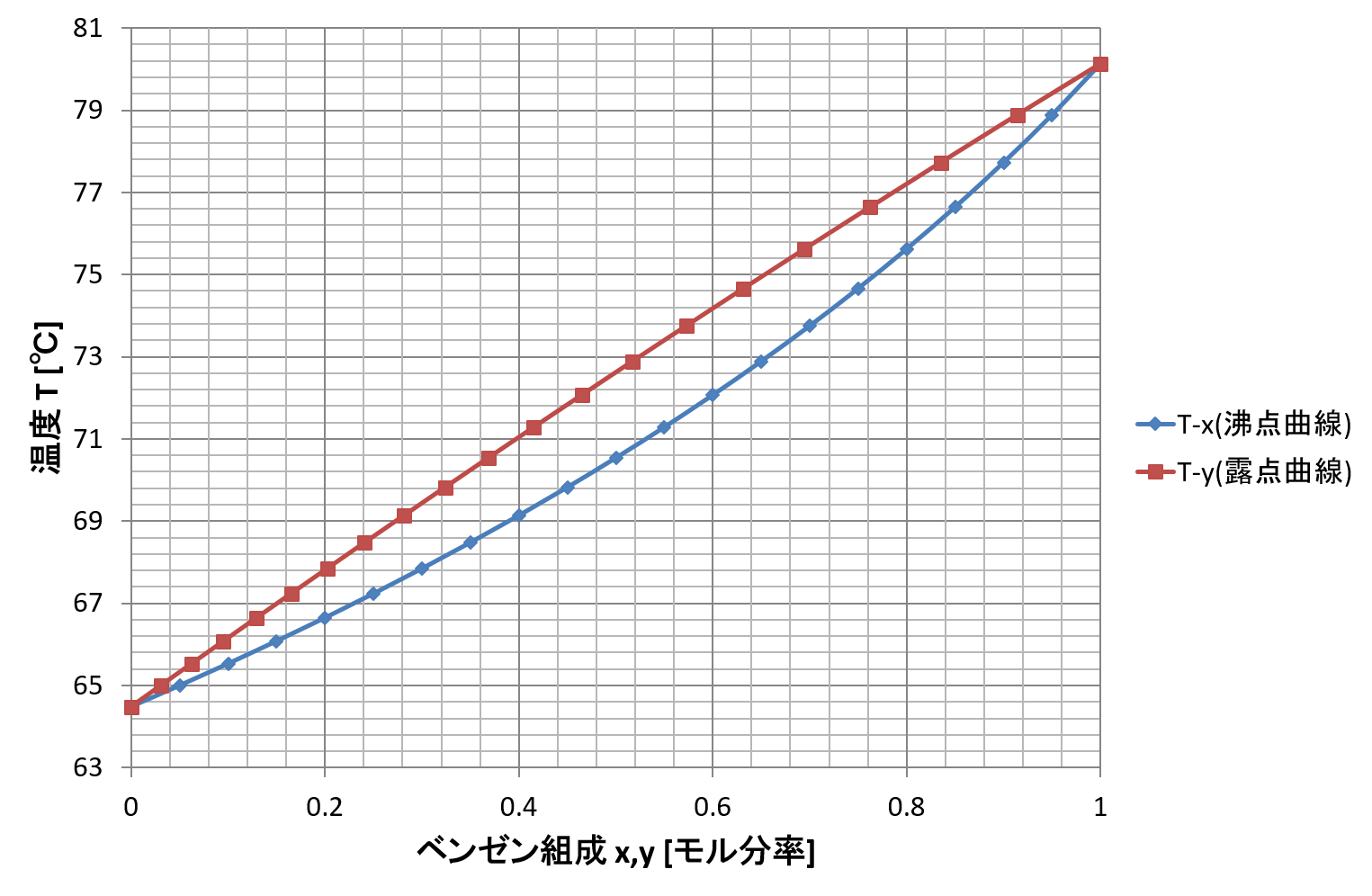
■NRTLモデルを用いたベンゼン-メタノール2成分系の大気圧下におけるT-xy線図(こちらが実測値に近い)
理想状態とNRTLモデルとでは気液平衡の挙動が大きく異なることがわかります。
仮にベンゼン-メタノール二成分系のプラントを設計する場合、気液平衡の推算モデルを「理想状態」として選択してしまうと、誤った計算結果が出力されてしまいます。配管、機器、計器全ての設計に大きく影響しますので、推算モデルの選択ミスはまず許されません。
だからと言って、活量係数モデルさえ選択すれば良いのではなく、このモデルも万能ではありません。
活量係数モデルは、成り立ちが理想状態の気液平衡であるRault式を拡張したモデルのため、低圧の極性物質の系では実測値とよく合いますが、高圧や石油・ガスプロセスの系では精度が悪くなることにご注意下さい。
状態方程式モデル
非理想性を表すためのもう一つのアプローチが状態方程式モデルです。
状態方程式モデルはその名の通り、気体の状態方程式を拡張、発展して生まれた気液平衡の推算モデルです。
<状態方程式>
$$PV=nRT$$
P:圧力
V:体積
n:モル数
R:気体定数
T:温度
状態方程式は理想気体においてのみ成り立つ式なので、実在気体では成り立ちません。
実在気体について成り立つように、状態方程式を拡張して考案されたのが、Van der Waals式(ファンデルワールス式)です。
<Van der Waals式>
$$P=\frac{RT}{V-b}-\frac{a}{V^2}$$
P:圧力
V:体積
R:気体定数
T:温度
a:Van der Waals定数(分子間力を表す定数)
b:Van der Waals定数(排除体積を表す定数)
Van der Waal式をPV線図で表すと以下のグラフのようになります。
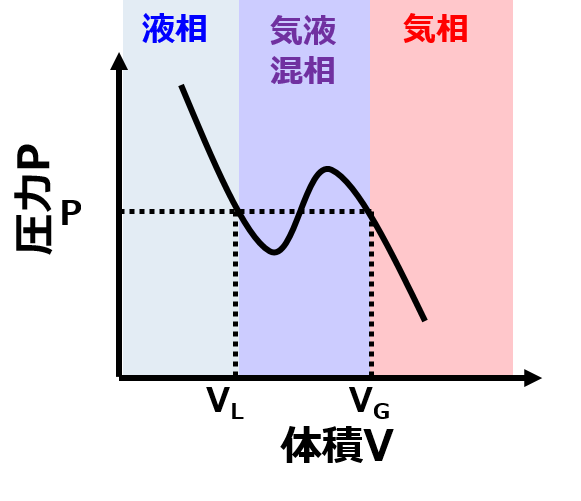
このグラフが意味することは、ある圧力範囲では対象流体が気液混相となり、小さい方の体積VLが液相の体積、大きい方の体積VGが気相の体積を表している、ということです。
よって、圧力と温度が分かれば、液相と気相の体積が求まるのですが、このままでは液相、気相の組成までは求められません。
ここで、フガシティの概念を導入します。
フガシティは圧力と同じ単位を持つ状態量の一つで、熱力学的圧力と呼ばれ、気液平衡においては、液相のフガシティと気相のフガシティは等しくなります。
また、液相(気相)のフガシティは圧力に液相(気相)のモル分率とフガシティ係数をかけたものです。
補足:フガシティは気液平衡における気体と液体の圧力の関係をうまく表現する時に便利な概念です。この記事では概念的な説明に留めますが、詳細については熱力学の教科書等を参照下さい。
<フガシティ>
$$f_L=f_G$$
$$f_L=φ_L*x_i*P$$
$$f_G=φ_G*y_i*P$$
fL:液相のフガシティ
fG:気相のフガシティ
φL:液相のフガシティ係数
φG:気相のフガシティ係数
xi:成分iの液相中のモル分率
yi:成分iの気相中のモル分率
P:圧力
また、フガシティ係数は液相、気相の体積から計算することが出来ます。純物質の場合は以下の計算式で求めることが出来ますが、混合物の場合は非常に複雑な式になります。ここでは、液相、気相の体積からそれぞれのフガシティが計算できる、ということだけ理解しておけば十分です。
【参考】<フガシティ係数の計算(純物質の場合)>
$$\ln{φ_L}=\int_0^P\biggl(\frac{V_L-V}{RT}\biggl)dP$$
$$\ln{φ_G}=\int_0^P\biggl(\frac{V_G-V}{RT}\biggl)dP$$
φL:液相のフガシティ係数
φG:気相のフガシティ係数
VL:液相の体積
VG:気相の体積
V:理想気体として求めた体積
P:圧力
R:気体定数
T:温度
したがって、ある圧力、温度において計算した液相、気相の体積から、液相と気相のフガシティが計算出来るようになりましたので、後は液相と気相のフガシティが等しい関係を利用すれば、液相、気相の組成を計算することが可能です。
計算手順をまとめると以下の通りになります。
計算手順
① 状態方程式(Van der Waals式など)を用いて、圧力から液相、気相の体積を計算
② 液相と気相のフガシティを計算
③ フガシティが等しい時の液相、気相のモル分率を計算
ここまでの解説では、なるべく単純化するために、Van der Waals式を用いましたが、実際の気液平衡の推算モデルでは、Van der Waals式をさらに拡張した式を推算モデルとして使用します。
よく使用される推算モデルはSRK式(Soave-Redlich-Kwong式)やPR式(Peng-Robinson式)です。
これらの推算モデルは基本的にはVan der Waals式に新たな補正項を導入することで、実測値に近づけたほか、フガシティ係数の計算において二成分相互パラメータを導入することで、より精度を上げています。
<SRK式>
$$P=\frac{RT}{V-b}-\frac{a}{V(V+b)}$$
<PR式>
$$P=\frac{RT}{V-b}-\frac{a}{V(V+b)+b(V-b)}$$
P:圧力
V:体積
R:気体定数
T:温度
a:温度と物質の種類の関数
b:物質定数
本記事では省略しますが、a,bを求めるには、推算の対象となる物質由来のパラメータから複雑な式を解く必要があります。二成分系ならまだしも多成分となると、もはや手計算で計算することが不可能に近いので、プロセスシミュレーターなどのツールの出番ということになります。
また、活量係数モデル同様に、状態方程式モデルも万能というわけではありません。
状態方程式モデルの成り立ちは理想気体の状態方程式(PV=nRT)で、それを拡張・発展させたものです。ベースとなるのは気体の計算で、それを気液平衡の計算が出来るように拡張させたものなので、高圧の石油・ガスプロセスの推算は実測値によく合いますが、低圧、極性物質の気液平衡の推算においては精度が悪くなります。
まとめ
この記事ではプラント設計で使用される気液平衡の推算モデルについて解説しました。
気液平衡の推算モデルは大きく分けると以下の2つに分けられます。
推算モデル
① 活量係数モデル
② 状態方程式モデル
それぞれの推算モデルでは得意、不得意な領域がありますので、うまく使い分ける必要があります。
また、最近のプロセスシミュレーターでは、これらの推算モデルを不得意領域を補うようにさらに拡張された推算モデルも実測されています。
例えば、状態方程式モデルの代表格であるSRK式の弱点であった極性物質の気液平衡の精度を上げるように開発された修正SRK式などがあります。これにより、高圧かつ極性物質の系においてもある程度高い精度で推算することが出来ます。
お使いのプロセスシミュレーターの説明書等で確認してみて下さい。
誤った推算モデルによるシミュレーションは誤った計算を結果を正としまう可能性があり、プラント全体の設計(機器設計、配管設計、計装設計)に大きく影響します。そのため、今回の記事で解説した概念はプロセス設計者(プロセスエンジニア)にとっては必須の知識です。
この記事が役に立てば幸いです。ではまた他の記事でお会いしましょう。
