
今回の記事では真空ポンプの排気時間の計算方法について解説します。
真空ポンプの設計、タイプの選定において最も重要なのは排気時間の計算です。この記事では、簡易的に計算する方法と厳密に計算する方法の2通りについて解説します。
合わせて読みたい
・【ポンプ】プラントで使用されるポンプ(Pump)の種類と特徴の解説
・【ポンプ】ポンプ運転時の注意事項と保守について
・【ポンプ】ポンプの設計、購入業務において規定すべき設計条件の解説
・【ポンプ】遠心ポンプの締め切り圧力(Shut-off Pressure)とは?設計圧力との関係
・【ポンプ】ポンプの設計・仕様確認で良く用いられる計算式の解説
・【ポンプ/圧縮機】プラントで使用される回転機の駆動源選定の主な検討事項について解説
・【圧縮機】コンプレッサー(Compressor)の種類と特徴の解説
・【圧縮機】あなたのプラントは大丈夫?遠心コンプレッサー周りのSettle out Pressureの説明・算出方法
・【圧縮機】遠心コンプレッサーのサージングとその対策方法について
・【タービン】化学プラントで使用される蒸気タービンの種類と特徴の解説
・【タービン】蒸気タービンの設計における適用規格と留意点の解説
・【気液平衡】プラント設計で使用される気液平衡の推算モデルの解説
・【移動現象】粒子の抵抗係数と終端速度の計算方法の解説
・【撹拌】Pv値とは?攪拌槽のスケールアップの留意点について解説
・【物性推算】沸点から蒸発熱、臨界温度を求める方法。「トルートンの規則」と「Guldbergの通則」について解説
・【物性推算】プロセスシミュレーションで使用される物性推算モデルの適用範囲の解説
・【蒸留塔】簡単に蒸留分離段数の目安を計算する方法の解説
・【熱交換器】多管式熱交換器(シェル&チューブ式)の流速、レイノルズ数の計算方法について解説
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】プラントで使用されるスプレーノズルの設計方法の解説
・【吸収塔】吸収塔高さの計算に必要な移動単位数(NTU)を図解法で求める方法の解説
・サットンの式とは?毒性ガス、可燃性ガスの着地濃度の計算方法について解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
・プラントのプロセス制御性と最適な制御方式の考え方について解説
・「濾過助剤」とは?プラントで使用される濾過助剤の種類と特徴について解説
・エジェクター(Ejector)の駆動空気量の算出方法について解説
簡易的な計算法
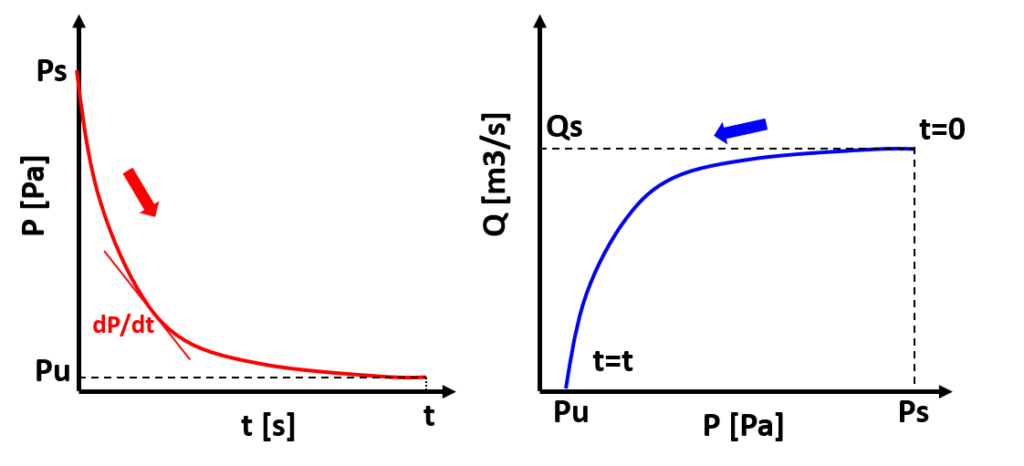
体積V[m]、圧力Ps[Pa]の容器を真空ポンプで排気するときの経時変化を上図に記しました。左側が圧力の経時変化、右側が排気速度の経時変化を表します。時に右側の曲線は排気曲線と呼ばれる曲線で、真空ポンプのカタログなどに必ず記載される重要なデータです。
初期圧力Psから排気を開始し、圧力が真空に近づくに従って、排気速度Q [m3/s]はだんたん小さくなるため、圧力の変化もだんだん小さくなり、ある圧力Puに到達したところでこれ以上真空には近づかなくなります。このPuは真空到達度、あるいは到達圧力と呼ばれ、真空ポンプの排気速度が0となる圧力で、真空ポンプの能力を表す重要な因子です。
数式モデル
簡単のため、排気速度Q [m3/s]は一定として漏れなどを無視すると、排気速度簡単容器内の圧力がP[Pa]のとき、微小時間dt [s]における圧力変化は、体積あたりの排気速度と真空到達度の積に等しいので、以下の等式が成り立ちます。
$$\frac{dP}{dt}=\frac{Q}{V}(P-P_u)$$
P:容器内圧力 [Pa]
Pu:真空到達度 [Pa]
t:時間 [s]
Q:排気速度 [m3/s]
V:容器の体積 [m3]
t=0の時P=Ps、t=tの時P=Pの境界条件で、この等式を積分して整理すると以下の通りになります。
$$t=\frac{V}{Qs}\ln{\biggl(\frac{P_s-P_u}{P-P_u}\biggl)}$$
P:容器内圧力 [Pa]
Ps:初期圧力[Pa]
Pu:真空到達度 [Pa]
t:時間 [s]
Q:排気速度 [m3/s]
V:容器の体積 [m3]
ただし、上図の排気曲線でも表示されている通り、実際の排気速度は圧力の関数となっているため、排気速度Qを一定とみなすのは無理があります。
そこで、初期圧力Psにおける排気速度Qsと減圧後の目的圧力Pにおける排気速度Qの平均値を一定とみなして、以下の通りに修正します。
$$t=\frac{V}{\frac{Q_s+Q}{2}}\ln{\biggl(\frac{P_s-P_u}{P-P_u}\biggl)}$$
P:容器内圧力 [Pa]
Ps:初期圧力[Pa]
Pu:真空到達度 [Pa]
t:時間 [s]
Q:圧力Pにおける排気速度 [m3/s]
Qs:初期圧力Psにおける排気速度 [m3/s]
V:容器の体積 [m3]
この数式が初期圧力Psから任意の圧力Pに減圧するまでの排気時間を求める計算式(簡易的な計算法)です。
排気曲線は真空ポンプのカタログ等で記載されているので、この曲線から任意の圧力における排気速度Q、Qsを読み取ります。また、真空到達度も同様にカタログなどから入手します。
この計算式でも排気速度の平均を一定として考えているため、実際の排気時間とはずれが生じますが、初期検討ではひとまずこの簡易法でも問題ありません。次項から厳密な計算法について解説します。
厳密な計算法
こちらの計算法は、真空ポンプの形式がレシプロ往復動ポンプ(往復動ポンプ)やロータリーポンプなどの容積型であることを利用します。
真空ポンプの排気曲線は必要ありませんが、ポンプの回転数(ストローク数)やチャンバー容積 [m3]が必要となります。
数式モデル
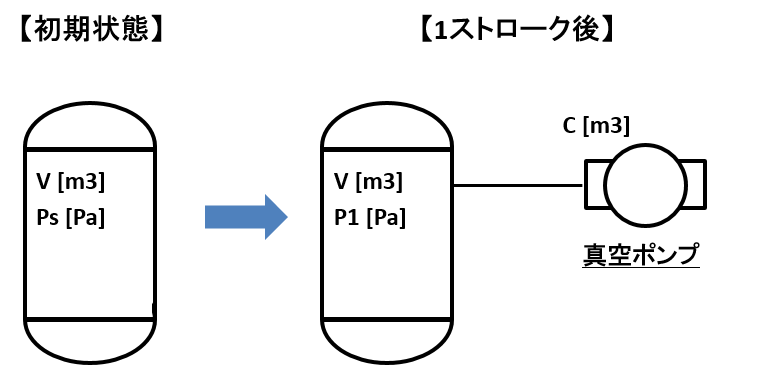
体積がV [m3]、初期圧力Ps [Pa]の容器があり、真空ポンプ(チャンバー容積C[m3])で1ストロークだけ減圧させた後の圧力をP1とすると、体積VからV+Cに膨張したと考え、理想気体のボイルの法則から、以下の等式が成り立ちます。
※減圧操作は負圧、常温なので、理想気体とみなして問題無い。
$$P_sV=P_1(V+C)$$
圧力P1から1ストローク減圧すると、以下の等式が成り立ちます。
$$P_1V=P_2(V+C)$$
さらに1ストローク減圧すると、以下の等式が成り立ちます。
$$P_2V=P_3(V+C)$$
n-1回目のストロークからn回目のストローク減圧すると以下の通りになります。
$$P_{n-1}V=P_n(V+C)$$
Ps:初期圧力[Pa]
Pn:nストローク後の容器内圧力 [Pa] (n=1~nの自然数)
V:容器の体積 [m3]
C:ポンプのチャンバー容積 [m3]
したがって、1ストローク後からnストローク後(n=1~nの自然数)のそれぞれの等式(上式)の両辺をかけ合わせると、P1~Pn-1は消去され、以下の通りになります。
$$P_sV^n=P_n(V+C)^n$$
$$\frac{P_n}{P_s}=\frac{V^n}{(V+C)^n}$$
両辺の対数をとって整理すると、
$$n=\frac{\ln{\biggl(\frac{P_n}{P_s}\biggl)}}{\ln{\biggl(\frac{V}{V+C}\biggl)}}$$
n:ストローク合計数
Ps:初期圧力[Pa]
Pn:nストローク後の容器内圧力 [Pa] (n=1~nの自然数)
V:容器の体積 [m3]
C:ポンプのチャンバー容積 [m3]
ここで、ストローク合計数はポンプの回転数(ストローク数)と時間の積なので、
$$n=R\times{t}$$
となり、
$$t=\frac{\ln{\biggl(\frac{P_n}{P_s}\biggl)}}{R\times\ln{\biggl(\frac{V}{V+C}\biggl)}}$$
と表せられます。
t:排気時間 [s]
R:ポンプ回転数 [rps]またはストローク数 [stroke/s]
Ps:初期圧力[Pa]
Pn:容器内圧力 [Pa]
V:容器の体積 [m3]
C:ポンプのチャンバー容積 [m3]
この数式により、ポンプの回転数またはストローク数、チャンバー容積の情報があれば、初期圧力から任意の圧力に減圧するまでの排気時間を計算で求めることができるようになりました。
こちらの計算法の方が簡易法よりも厳密に排気時間を計算することが可能です。
なお、ポンプの回転数またはストローク数、チャンバー容積は真空ポンプのカタログやポンプメーカーから入手することが可能です。
計算例
30L(0.03 m3)の容器を大気圧から1.5Paまで減圧することを考えます。
前提として以下の情報が入手済みであると仮定します。
前提条件
大気圧における排気速度(初期排気速度)Qs:0.0024 m3/s
1.5Paにおける排気速度 Q:0.0012 m3/s
真空到達度 Pu:0.8 Pa
ポンプ回転数 R:12 rps
チャンバー容積 C:0.0002 m3
簡易法と厳密法それぞれで排気時間を計算します。
簡易法
$$t=\frac{V}{\frac{Q_s+Q}{2}}\ln{\biggl(\frac{P_s-P_u}{P-P_u}\biggl)}$$
簡易的な計算法である上式に各条件を代入すると、以下の通りになります。
$$t=\frac{0.03}{\frac{0.0024+0.0012}{2}}\ln{\biggl(\frac{101325-0.8}{1.5-0.8}\biggl)}=203$$
よって、排気時間t=203秒と計算されました。
厳密法
$$t=\frac{\ln{\biggl(\frac{P_n}{P_s}\biggl)}}{R\times\ln{\biggl(\frac{V}{V+C}\biggl)}}$$
厳密な計算法である上式に各条件を代入すると、以下の通りになります。
$$t=\frac{\ln{\biggl(\frac{1.5}{101315}\biggl)}}{12\times\ln{\biggl(\frac{0.03}{0.03+0.0002}\biggl)}}=143$$
よって、排気時間t=143秒と計算されました。
簡易法と厳密法とでは60秒程度の差異があることが分かります。
まとめ
今回の記事では真空ポンプの排気時間の計算方法について解説しました。
真空ポンプの設計、タイプの選定において最も重要なのは排気時間の計算ですが、簡易的に計算する方法と厳密に計算する方法の2通りがあります。入手可能な情報や状況に応じて使い分けてみてください。
この記事が役に立てば幸いです、ではまた他の記事でお会いしましょう。