
今回の記事では攪拌槽のスケールアップの留意点について解説します。また、この時の重要なパラメータである「Pv値」の使い方についても合わせて解説します。
ラボスケール(数百ml~数L)から実機プラントスケール(数m3以上)までスケールアップする際は、ベンチプラント、パイロットプラントなどの中試験を経て順にスケールアップされます。本記事では適切にスケールアップを行うことができるよう、留意しておくべき項目について解説します。
合わせて読みたい
・プロセスエンジニアって何をする仕事?
・プラントエンジニアはブラックか?プラント設計概要と共に解説
・化学工学ってプラントエンジニアリングのどんな場面で使われる?
・化学メーカーとプラントエンジニアリング会社はどう違う?【就職・転職】
・横型タンクの内容量の計算方法の解説~タンクテーブルの作成~
・縦型タンクの内容量の計算方法、タンクテーブルの作成方法
・タンク,ドラムの液面計ノズル位置と滞留時間の決め方の解説
・【気液平衡】プラント設計で使用される気液平衡の推算モデルの解説
・【移動現象】粒子の抵抗係数と終端速度の計算方法の解説
・【回転機】真空ポンプの排気時間の計算方法の解説
・タンク、ベッセルの排水時間の計算方法の解説
・【物性推算】沸点から蒸発熱、臨界温度を求める方法。「トルートンの規則」と「Guldbergの通則」について解説
・【物性推算】プロセスシミュレーションで使用される物性推算モデルの適用範囲の解説
・【蒸留塔】簡単に蒸留分離段数の目安を計算する方法の解説
・【熱交換器】多管式熱交換器(シェル&チューブ式)の流速、レイノルズ数の計算方法について解説
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】プラントで使用されるスプレーノズルの設計方法の解説
・【吸収塔】吸収塔高さの計算に必要な移動単位数(NTU)を図解法で求める方法の解説
・サットンの式とは?毒性ガス、可燃性ガスの着地濃度の計算方法について解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
・プラントのプロセス制御性と最適な制御方式の考え方について解説
・「濾過助剤」とは?プラントで使用される濾過助剤の種類と特徴について解説
すりつぶし効果

出典:funakoshi
ラボスケールにおける攪拌操作はマグネチックスターラーを用いることが多いですが、固液系のスラリーを攪拌する時は、固体が攪拌子(スターラーバー)によりすりつぶされて微粒子化してしまうことがあります。
この時、固体触媒による不均一反応を行っている場合は触媒の微粒子化により反応効率が上がり、反応が速く進行してしまう場合があります。
攪拌槽による攪拌ではこのようなことは発生しませんから、これに気付かずにスケールアップをしてしまうと同じ反応条件でも思ったより反応が進まず、性能未達となってしまう可能性があります。
そのため、特に固体触媒による不均一反応を攪拌で行う場合は、すりつぶし効果によって正しくデータが採取できない可能性を考慮しておく必要があります。
スケール効果
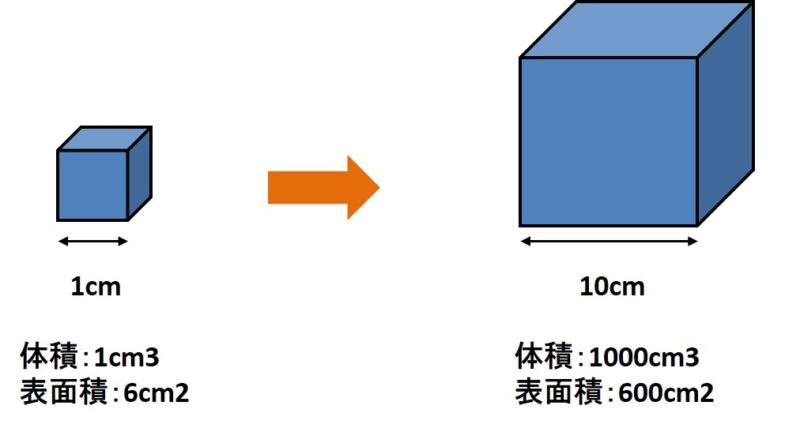
攪拌のようなバッチ操作のスケールアップでは、体積が大きくなっても面積は同程度には大きくならないことに留意しておく必要があります。
例えば、サイコロの様な立方体を1cm角から10cm角にスケールアップすることを考えます。
まず、1cm角の立方体の体積は1cm3で表面積は6cm2となります。
一方、10cm角の立方体の体積は1000cm3で表面積は600cm2となります。
この時、体積は10^3=1000倍になっているのに対し、表面積は10^2=100倍にしか大きくなっていないことが分かります。
また、それぞれの立方体において発熱反応が起こると仮定した場合、発熱量は体積に比例し、除熱量は表面積に比例します。
上記のスケールアップでは発熱量は1000倍になるのに対し、除熱量は100倍にしかなりません。実際のスケールアップに当てはまると、ラボスケールでは発熱と除熱がバランスしており、問題にならなかったのに対し、パイロットプラントスケールでは除熱が追い付かず、温度上昇が問題となってスケールアップの失敗となってしまいます。
このようにスケールアップした際に初めて問題が認識されることをスケール効果と呼びます。スケール効果は熱移動だけでなく、様々な項目で発生する可能性があるため、十分に留意しておく必要があります。
主なスケール効果
・伝熱(加熱、発熱、除熱)
・攪拌槽内の発泡(フォーミング)
・攪拌槽壁面へのスケーリング
・分液時のエマルジョン
・濾過(ケーキ厚み増加による圧密効果)
Pv値
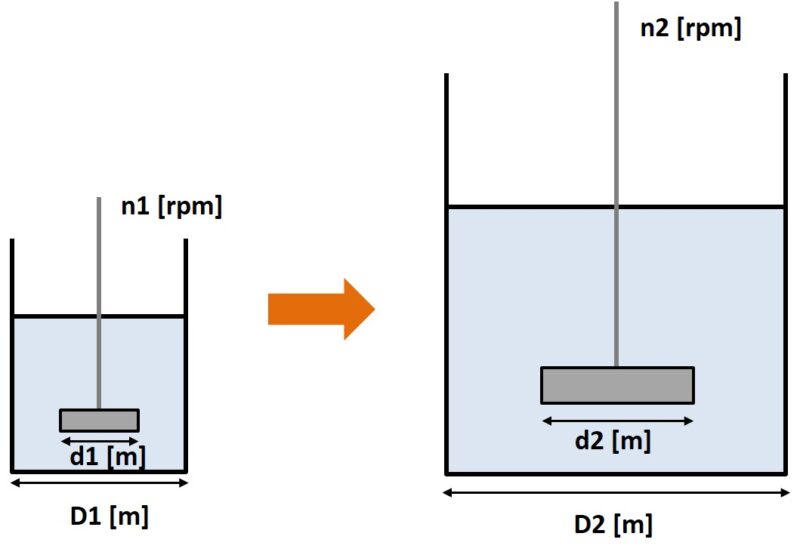
攪拌槽のスケールアップで最も重要なのはPv値です。
Pv値は攪拌槽の単位体積あたりの撹拌機動力(P/V [kW/m3])を表し、通常のスケールアップではPv値を一定となります。
また、Pv値は概ね1.0程度(1m3あたりの動力が1kW)で、ポリマーなどを扱う攪拌槽だと、5.0程度になることもあります。
撹拌機の動力は回転数と動力数Npで表すことができ、Pv値は以下の関係式から求めることができます。
<動力数Np>
$$N_p=\frac{P}{ρn^3d^5}$$
$$P=N_pρn^3d^5$$
Np:動力数 [-]
P:動力 [W]
ρ:液密度 [kg/m3]
n:回転数 [1/s]
d:攪拌翼直径 [m]
<Pv値(P/V)>
$$V∝D^3$$
なので
$$\frac{P}{V}∝\frac{N_pρn^3d^5}{D^3}=N_pρ\biggl(\frac{d^3}{D^3}\biggl)n^3d^2$$
と変形。
ここで、乱流では動力数Np一定、ρ一定、相似な攪拌槽でd/D一定なので、以下のように表すことができます。
$$N_pρ\biggl(\frac{d^3}{D^3}\biggl)n^3d^2∝n^3d^2$$
したがって
$$\frac{P}{V}∝n^3d^2=一定$$
となります。
つまり、Pv値(P/V)が一定ということは、n^3d^2が一定となるように回転数nを決めれば良いということになります。
実際のスケールアップでは、回転数だけでなく撹拌機の動力まで求める必要がありますが、上記の動力数Npの関係式を用いて求めることができます。
攪拌フルード数とせん断力
攪拌フルード数
固液のスラリーをスケールアップする場合は、個体粒子と液の比重差の影響を考慮する場合があります。
そのような場合には攪拌フルード数Frが一定となるようにスケールアップする必要があります。
<攪拌フルード数>
$$Fr=\frac{n^2d}{g}∝n^2d=一定$$
Fr:攪拌フルード数 [-]
n:回転数 [1/s]
d:攪拌翼直径 [m]
g:重力加速度 [m/s2]
つまり、攪拌フルード数が一定ということは、n^2dが一定となるように回転数nを決めれば良いということになります。
せん断力
固液のスラリー系で特に強度の弱い結晶を攪拌する場合には、翼先端のせん断力τが一定となるようにスケールアップする必要があります。
<せん断力>
$$τ=πnd∝nd=一定$$
τ:せん断力 [m/s]
n:回転数 [1/s]
d:攪拌翼直径 [m]
つまり、せん断力が一定ということは、ndが一定となるように回転数nを決めれば良いということになります。
計算例
密度950kg/m3の液体が2m3のバッフル付き攪拌槽に仕込まれ、6枚平板タービン翼(直径0.51m)、回転数120rpmで攪拌(効率は90%)されている時、同じタービン翼で直径を2mにスケールアップすることを検討します。
回転数
Pv値一定でスケールアップするため、n^3d^2が一定となるように回転数を求めます。
<Pv値一定>
$$n^3d^2=N^3D^2$$
なので、それぞれ条件を代入すると、
$$(120/60)^3\times{0.51}^2=N^3\times2^2$$
n:回転数 [1/s]
d:攪拌翼直径 [m]
N:回転数(スケールアップ後) [1/s]
d:攪拌翼直径(スケールアップ後)[m]
これを解いて
$$N≒0.804 [1/s]≒48.2 [rpm]$$
従って、スケールアップ時の回転数は48.2 rpmと求めることができました。
なお、攪拌フルード数一定、せん断力一定とした場合の回転数は以下の通りです。
<攪拌フルード数一定>
$$n^2d=N^2D$$
$$N≒1.01 [1/s]≒60.6 [rpm]$$
<せん断力一定>
$$nd=ND$$
$$N=0.51 [1/s]≒30.6 [rpm]$$
動力
簡単のために、攪拌レイノルズ数が十分に大きく乱流であると仮定します。
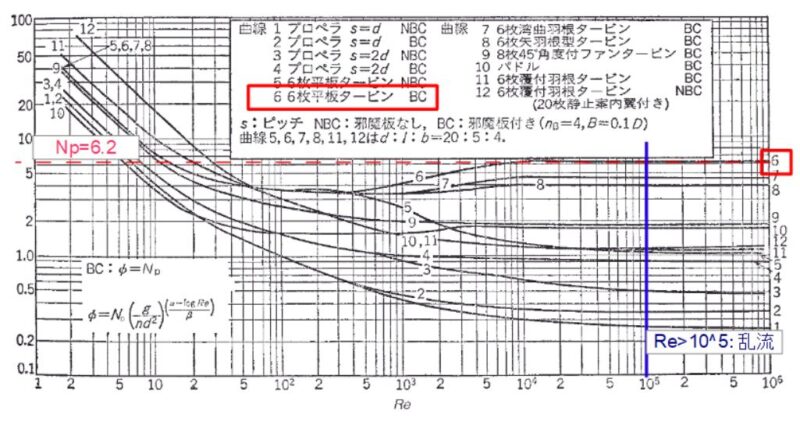
出典:化学工学便覧第6版
上図から読み取ると、バッフル付きの6枚平板タービン翼では乱流域においては動力数Np=6.2となります。
$$N_p=\frac{P}{ρn^3d^5}$$
の関係を用いてスケールアップ前後における動力を計算すると以下の通りです。
※数式表示が途切れている場合はスライドすると表示されます。
<スケールアップ前>
効率は90%なので、
$$P_a=\frac{P}{η}=\frac{1.6}{0.9}=1.8 [kW]$$
<スケールアップ後>
$$P_a=\frac{P}{η}=\frac{97.7}{0.9}=109 [kW]$$
Np:動力数 [-]
P:動力 [W]
Pa:実動力 [W]
ρ:液密度 [kg/m3]
n:回転数 [1/s]
d:攪拌翼直径 [m]
η:撹拌機効率 [-]
従って、スケールアップ前の動力は1.8kW、スケールアップ後の動力は109kWと計算することができました。
なお、仮にスケールアップ前後の回転数を一定(120rpm)とすると、スケールアップ後の動力は1675kWとなります。この数値は大型プラントの圧縮機に匹敵するような大きな動力なので、この程度の撹拌機の動力としてはあまりにも大きく、非現実的な動力となってしまいます。
Pv値
最後にPv値も求めておきます。
Pv値は単位体積あたりの動力なので、
$$\frac{P}{V}=\frac{1.8}{2}=0.9$$
となり、1.0前後の値なので妥当であることが分かります。
まとめ
今回の記事では攪拌槽のスケールアップの留意点について解説しました。
スケールアップの留意点
・ すりつぶし効果
・ スケール効果
・ Pv値
・ 攪拌フルード数、せん断力
特にPv値は攪拌槽のスケールアップにおいて重要な考え方なので、ぜひ覚えるようにして下さい。
この記事が役に立てば幸いです。ではまた他の記事でお会いしましょう。