
今回の記事では気液二相流の圧力損失の計算方法について解説します。
気液二相流の圧力損失は、最近ではプロセスシミュレーターを用いて計算することがほとんどですが、今回の記事では手計算で二相流の圧力損失を計算する方法について解説します。
手計算で二相流の圧力損失を計算する場合は、以下の計算式のLockhart&Martinelliの方法が一般的です。
<Lockhart&Martinelliの方法>
$$ΔP=φ^2ΔP_V$$
$$φ=f(X)$$
φは混相流パラメータと呼ばれ、Lockhart-Martinelli Moduleと呼ばれる変数Xの関数で表されます。また、流動状態によって異なる計算式となります。(後述)
Lockhart-Martinelli ModuleのXは以下の式から算出されます。
$$X^2=\biggl(\frac{W_L}{W_V}\biggl)^{1.8}\biggl(\frac{ρ_V}{ρ_L}\biggl)\biggl(\frac{μ_L}{μ_V}\biggl)^{0.2}$$
垂直上昇流の場合、Xの代わりにDavisの補正項Xdを用います。
$$X_d=0.19X{Fr}^{0.185}$$
$$Fr=\frac{U^2}{gD}$$
ΔP:気液二相流の圧力損失 [kg/cm2]
ΔPV:気体のみが流れる場合の圧力損失 [kg/cm2]
φ:混相流パラメータ(流動状態による)
X:Lockhart-Martinelli Module
Xd:Davisの補正項
WV:気相の流量 [kg/h]
WL:液相の流量 [kg/h]
ρV:気相の密度 [kg/m3]
ρL:液相の密度 [kg/m3]
μV:気相の粘度 [cP]
μL:液相の粘度 [cP]
Fr:Froude数 [-]
U:二相流の平均流速 [m/s]
g:重力加速度=9.8 [m/s2]
D:配管内径 [m]
まず二相流の気、液の流量や物性からLockhart-Martinelli ModuleのXを求め、混相流パラメータのφを算出し、そこから二相流の圧力損失を計算する手順となります。
この手順は二相流の流動状態に応じて若干異なりますが、大まかな計算手順としては同じです。
こちらの記事では二相流の流動状態について解説していますので合わせてご確認ください。
次項から各流動状態の圧力損失の計算方法について解説します。
ただし、配管径が2 1/2インチ以下の小口径の場合は流動状態によらず噴霧流として圧力損失を計算します。
合わせて読みたい
・【配管】家庭用水道管の凍結防止対策に対する定量評価
・【配管】機器周りの配管レイアウト設計の留意点について解説
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】プラントの音響疲労破壊とは?音響レベルの計算方法と対策
・【配管】プラントの配管振動を引き起こす主な原因とその対策について
・【配管】プラント建設後の配管はどうやって洗浄する?配管洗浄方法の解説
・【配管】ラインチェックとは?プラント配管施工時の確認項目について解説
・【配管】マニュアルバルブ(手動弁)の選定基準について解説
・【配管】プラント配管の主な構成要素について解説
・【配管】プラントの配管設計における一般的な留意事項について解説
・【配管】気液二相流の流動状態(フローパターン)とその判定方法について解説
・【材質】配管の材質はどうやって決まる?配管材料選定の留意点について解説
・【材質】応力緩和割れとは?オーステナイト系ステンレス鋼の注意点
・【材質】ステンレスが水で腐食する?微生物腐食の原理と対策
・【材質】水素配管の材質は炭素鋼?ステンレス鋼?水素浸食と水素脆性について解説
二層流(Stratified Flow)
二層流の混相流パラメータφは以下の式から算出します。
<二層流の混相流パラメータ>
$$φ=\frac{54800X}{(W_L/A)^{0.8}}$$
φ:混相流パラメータ
X:Lockhart-Martinelli Module
WL:液相の流量 [kg/h]
A:配管断面積 [m2]
ただし、この流れは十分長い水平配管で起こる状態のため、二層流の流動状態でも環状流として圧力損失を計算することもあります。(後述)
波状流(Wavy Flow)
波状流については、混相流パラメータを用いず、Huntington相関係数Hxを用います。また、冒頭で解説したLockhart&Martinelliの方法ではなく、Huntington相関係数Hxから摩擦損失fを計算し、そこからファニングの式を用いて圧力損失を計算します。
<波状流の圧力損失の計算法>
$$H_X=(\frac{W_L}{W_V})(\frac{μ_L}{μ_V})$$
$$f=0.0185{H_X}^{0.211}$$
$$ΔP=\frac{2f{G_V}^2L}{gDρ_V}$$
Hx:Huntington相関係数
WL:液相の流量 [kg/h]
WV:気相の流量 [kg/h]
μV:気相の粘度 [cP]
μL:液相の粘度 [cP]
f:摩擦係数
Gv:気体の質量速度 [kg/m2s]
L:配管相当長 [m]
g:重力加速度=9.8 [m/s2]
D:配管内径 [m]
ρV:気相の密度 [kg/m3]
この流れも十分長い水平配管で起こる状態のため、波状流の流動状態でも環状流として圧力損失を計算することもあります。(後述)
環状流(Annular Flow)
環状流の混相流パラメータφは以下の式から算出します。
<環状流の混相流パラメータ>
$$φ=(4.8-0.123d)X^{0.343-0.000827d}$$
φ:混相流パラメータ
X:Lockhart-Martinelli Module
d:配管内径 [mm]
※10インチ以上の場合は一律d=250mmとする。
ただし、Lockhart-Martinelli ModuleのXよりDavisの補正項Xdの方が大きい場合はXdを代入してφを計算します。
気泡流(Bubble or Froth Flow)
気泡流の混相流パラメータφは以下の式から算出します。
<気泡流の混相流パラメータ>
$$φ=\frac{16.64X^{0.75}}{(W_L/A)^{0.1}}$$
φ:混相流パラメータ
X:Lockhart-Martinelli Module
WL:液相の流量 [kg/h]
A:配管断面積 [m2]
気泡流でもLockhart-Martinelli ModuleのXよりDavisの補正項Xdの方が大きい場合はXdを代入してφを計算します。
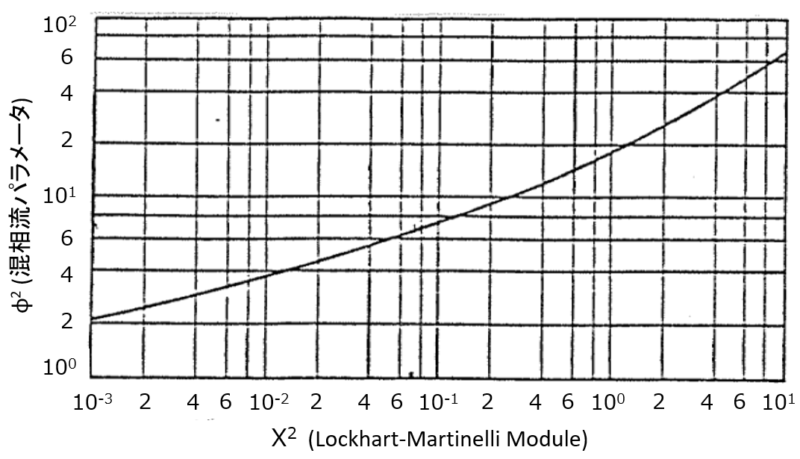
噴霧流(Dispersed Flow)
噴霧流はLockhart-Martinelli ModuleのXをもとに、下図から混相流パラメータφを読み取ります。
塊状流(Slug Flow)
塊状流の混相流パラメータφは以下の式から算出します。
<塊状流の混相流パラメータ>
$$φ=\frac{2630X^{0.815}}{(W_L/A)^{0.5}}$$
φ:混相流パラメータ
X:Lockhart-Martinelli Module
WL:液相の流量 [kg/h]
A:配管断面積 [m2]
栓流(Plug Flow)
栓流の混相流パラメータφは以下の式から算出します。
<塊状流の混相流パラメータ>
$$φ=\frac{35.8X^{0.855}}{(W_L/A)^{0.17}}$$
φ:混相流パラメータ
X:Lockhart-Martinelli Module
WL:液相の流量 [kg/h]
A:配管断面積 [m2]
