
今回の記事ではスパージャーの設計方法について解説します。
スパージャーは一般的にドラムやタンクの液中にガスや液を吹き込む装置のことで、吹き込んだ流体の運動エネルギーによって液を攪拌し、混合・反応・吸収といった単位操作を促進する役割があります。
一例として、空気を吹き込んで酸化反応を促進するための気泡塔や、タンク内の水に蒸気を吹き込んで水の温度を一定に保つことなどに使用されます。
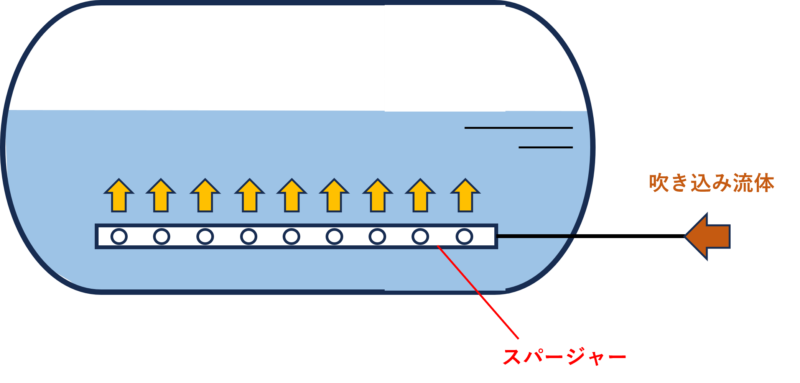
構造としては、パイプの端だけが開いたシンプルなものから、ドラムの底に多孔板を置くタイプまで様々なものがあります。ここではスパージャーの構造として最も一般的な、水平なパイプに複数の孔を開けた構造(下図)のものについて解説します。
合わせて読みたい
【配管】制限オリフィス孔径の計算手順の解説
【配管】液ラインの制限オリフィス孔径の簡易式とキャビテーション指数について
【配管】オリフィスの流量係数とは?形状との関係について解説
【配管】放熱計算による配管が凍結するまでの時間の推定-伝熱モデルの解説-
【配管】プラントで使用されるストレーナーの種類と特徴の解説
【配管】プラントで使用される減温器(デスーパーヒーター)の種類と特徴の解説
【配管】プラント配管で使用されるエキスパンションジョイントの種類と特徴の解説
【配管】プラントで使用されるスチームトラップの種類と特徴の解説
【配管】プラントで使用されるスプレーノズルの設計方法の解説
【配管】家庭用水道管の凍結防止対策に対する定量評価
・エジェクター(Ejector)の駆動空気量の算出方法について解説
設計方針
スパージャーの設計とは、孔の数を決めることと、孔径を求めることになりますが、設計にあたりもっとも重要なパラメータはスパージャーの吹き出し孔における圧力損失です。
スパージャーの性能として求められるのは、吹き出し孔からの流体が均一に流出することですが、一般に吹き出し孔における圧損を大きくすればするほど均一な流体分布になります。しかし、吹き出し孔の圧損を大きくしすぎると、吹き出し流体の必要圧力も大きくなってしまうので、ある程度の圧力があれば十分です。
一般に、スパージャーの吹き出し孔の必要圧力損失の条件は次の通りです。
吹き出し孔の必要圧力損失
(1) 主管における吹き出し流体の動圧の10倍以上
(2) 主管における吹き出し流体の圧力損失の10倍以上
上記を数式で表現すると以下の通りです。
<条件(1)>
$$ΔP_o≧\frac{1}{2}ρ{v_p}^2×10$$
<条件(2)>
$$ΔP_o≧ΔP_p×10$$
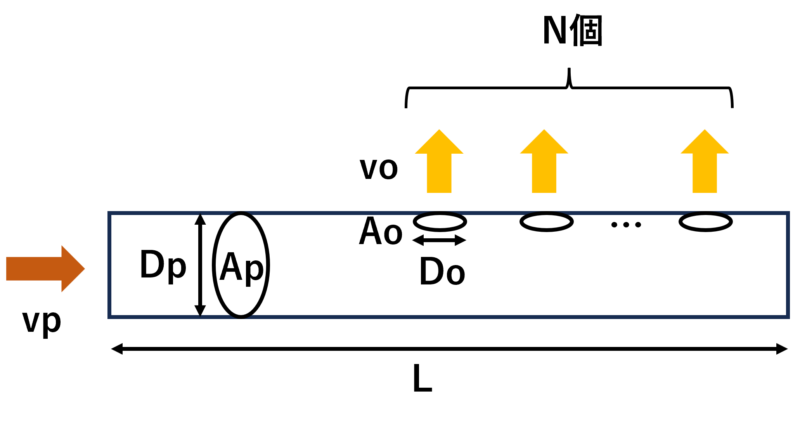
ΔPo:吹き出し孔での圧力損失 [Pa]
Do:吹き出し孔径 [m]
Ao:吹き出し孔の面積 [m2]
vo:吹き出し孔における流速 [m/s]
ΔPp:主管での圧力損失 [Pa]
Dp:主管の管径 [m]
Ap:主管の断面積 [m2]
vp:主管における流速 [m/s]
L:主管長さ [m]
N:孔の数 [-]
ρ:吹き出し流体の密度 [kg/m3]
つまり、上式を満足するような孔径Do[m]と孔の数N[-]を求めることに帰着されます。
次項から詳しく解説していきます。
条件(1)による設計
スパージャーの孔をオリフィスとみなし、オリフィスの設計式から以下の式が成り立ちます。
$$Q=\frac{A_o}{\sqrt{1-\biggl(\frac{D_o}{D_p}\biggl)^4}}×\sqrt{\frac{2ΔP_o}{ρ}}$$
Q:流量 [m3/s]
C:流量係数 [-]
ΔPo:吹き出し孔での圧力損失 [Pa]
Do:吹き出し孔径 [m]
Ao:吹き出し孔の面積 [m2]
Dp:主管の管径 [m]
Ap:主管の断面積 [m2]
ρ:吹き出し流体の密度 [kg/m3]
上式を変形して
$$ΔP_o=\biggl(\frac{1}{C^2}\biggl)\biggl(\frac{Q}{A_o}\biggl)^2\biggl(1-\biggl(\frac{D_o}{D_p}\biggl)^4\biggl)\biggl(\frac{1}{2}ρ\biggl)$$
ここで
$$v_o=\biggl(\frac{Q}{A_o}\biggl)$$
なので
$$ΔP_o=\biggl(\frac{1}{C^2}\biggl)\biggl(\frac{1}{2}ρ{v_o}^2\biggl)\biggl(1-\biggl(\frac{D_o}{D_p}\biggl)^4\biggl)$$
これを条件(1)式に代入すると
$$\biggl(\frac{1}{C^2}\biggl)\biggl(\frac{1}{2}ρ{v_o}^2\biggl)\biggl(1-\biggl(\frac{D_o}{D_p}\biggl)^4\biggl)≧\frac{1}{2}ρ{v_p}^2×10$$
ここで、流量係数C=0.61代入、かつ
$$Q=v_o\frac{π}{4}{D_o}^2=v_pN\frac{π}{4}{D_p}^2$$
の関係を用いて整理すると、
$$D_o≦\frac{D_p}{(1+3.721N^2)^{1/4}}$$
Do:吹き出し孔径 [m]
Dp:主管の管径 [m]
N:孔の数 [-]
となります。つまり、条件(1)は上式を満足するように吹き出し孔の径、孔数を決める必要があります。
また、上式を簡略化し、
$$D_o<0.72\frac{D_p}{\sqrt{N}}$$
を使用することもあります。
なお、流量係数についてはこちらの記事も参照ください。
条件(2)による設計
主管の圧力損失ΔPpはダルシー・ワイズバッハの式(またはファニングの式)より、次のようになります。
$$ΔP_p=f\frac{L}{D_p}\frac{1}{2}ρ{v_p}^2$$
ΔPp:主管の圧力損失
f:摩擦損失係数 [-]
Dp:主管の管径 [m]
vp:主管における流速 [m/s]
L:主管長さ [m]
ρ:吹き出し流体の密度 [kg/m3]
これを条件(2)式に代入(ΔPoについては条件(1)導出時のものと同じ)すると、
$$f\frac{L}{D_p}=\frac{{v_p}^2}{2}≦0.26875\biggl(\frac{v_o}{2}\biggl)^2\biggl(1-\biggl(\frac{D_o}{D_p}\biggl)^4\biggl)$$
さらに整理して、
$$D_o≦\frac{D_p}{\biggl(1+3.721f\frac{L}{D_pN^2}\biggl)^{1/4}}$$
Do:吹き出し孔径 [m]
f:摩擦損失係数 [-]
Dp:主管の管径 [m]
L:主管長さ [m]
N:孔の数 [-]
となります。これが条件(2)における孔径、孔数を算出する数式となります。
孔径、孔数を求めるためには条件(1)、条件(2)を両方満足する必要がありますが、条件(1)と条件(2)との近いはfL/Dp項の有無のみです。fL/Dp>1の場合は条件(2)の方が制約条件となりますが、ほとんどの場合ではfL/Dp<1となるので、条件(1)式のみがスパージャーの設計に影響することになります。
(fL/Dp>1となるのはLが大きくなる、即ち大型のドラムの場合)
例題
径が1mのドラムに主管が2インチ、長さ0.8m、孔数20のスパージャーで流量50m3/hで流体を供給することを考え、このときの孔径を算出します。
まず、この条件下では摩擦損失係数f=0.029となり、fL/Dp=0.46<1なので、条件(1)のみを考慮すれば問題ありません。
(摩擦損失係数の算出は省略。コールブルックの式等を用いて別途算出してください。)
Dp=0.05 [m], N=20を条件(1)式に代入すると、
$$D_o≦\frac{D_p}{(1+3.721N^2)^{1/4}}=\frac{0.05}{(1+3.721×20^2)^{1/4}}≒0.00805$$
となるので、孔径Doは0.008m(8mm)で良いということになります。
なお、スパージャーの孔径は一般的に3-13mm程度と言われています。
この記事が役に立てば幸いです。ではまた他の記事でお会いしましょう。

