
今回の記事ではウォーターハンマー(水撃)発生時の水撃圧の計算方法について解説します。
タンクやドラムから液体をポンプで輸送する場合、バルブの開閉やポンプの起動、停止などにより配管内の液流量が変動し、特有の圧力変動を起こし、これをウォーターハンマー(水撃)と呼びます。
この時発生する最大圧力(水撃圧)はサージ圧とも呼ばれ、通常運転中の圧力よりもはるかに大きいため、様々な設備トラブルの原因となります。
ウォーターハンマー(水撃)による主なトラブル
・過度な圧力上昇による設備の変形破損
・過度な圧力降下による大径管/ライニング管の座屈/損傷
・頻繁な水撃発生による設備の疲労損傷
・ポンプ/原動機などの逆回転/オ-バ-ランによる軸や軸受などの損傷
・水槽/タンク等の水面波打ちやオ-バ-フロ-などによる影響
・衝撃圧やこれに伴う振動によるガスケット類の損耗や継手漏洩
・衝撃圧やこれに伴う振動による計器類の機能障害/誤作動
特にLNGの出荷/受入基地やパイプラインで液体を長距離輸送する設備の場合は水撃圧を計算し、必ずこれを考慮した設計圧力にしなければなりません。そこで本記事ではJoukowskiの式(ジューコフスキーの式)やAllieviの式(アリエビの式)を用いたウォーターハンマー(水撃)発生時の水撃圧の計算方法について解説します。
合わせて読みたい
・【配管】家庭用水道管の凍結防止対策に対する定量評価
・【配管】機器周りの配管レイアウト設計の留意点について解説
・【配管】エロージョン速度とは?エロージョンを引き起こす配管流速について解説
・【配管】プラントの音響疲労破壊とは?音響レベルの計算方法と対策
・【配管】プラントの配管振動を引き起こす主な原因とその対策について
・【配管】プラント建設後の配管はどうやって洗浄する?配管洗浄方法の解説
・【配管】ラインチェックとは?プラント配管施工時の確認項目について解説
・【配管】マニュアルバルブ(手動弁)の選定基準について解説
・【配管】プラント配管の主な構成要素について解説
・【配管】プラントの配管設計における一般的な留意事項について解説
・【配管】気液二相流の流動状態(フローパターン)とその判定方法について解説
・【配管】気液二相流の圧力損失の計算方法について解説
・【材質】配管の材質はどうやって決まる?配管材料選定の留意点について解説
・【材質】応力緩和割れとは?オーステナイト系ステンレス鋼の注意点
・【材質】ステンレスが水で腐食する?微生物腐食の原理と対策
・【材質】水素配管の材質は炭素鋼?ステンレス鋼?水素浸食と水素脆性について解説
計算手順
急閉鎖か緩閉鎖の判定
水撃圧の計算方法は、対象が急閉鎖か緩閉鎖かのどちらかによって変わるため、急閉鎖か緩閉鎖かを判定する必要があります。
急閉鎖/緩閉鎖の判定手順
① 圧力伝播速度の計算
② 圧力波の往復時間の計算
③ バルブの有効ストローク時間(有効弁閉鎖時間)の計算
④ ②と③を比較
圧力伝播速度の計算
圧力伝播速度は以下の式から計算されます。
<圧力伝播速度の計算>
$$a=\frac{1}{\sqrt{γ\bigl(\frac{1}{K}+\frac{1}{E}\frac{D}{t}C\bigl)}}$$
a:圧力伝播速度 [m/s]
γ:液密度 [kg/m3]
K:流体の体積弾性係数 [kgf/m2]
C:配管拘束係数 (=通常1.0)
E:配管材のヤング率 [kgf/m2]
D:配管内径 [mm]
t:配管肉厚 [mm]
圧力波の往復時間の計算
圧力波の往復時間は以下の式から計算されます。
<圧力波の往復時間の計算>
$$μ=\frac{2L_a}{a}$$
μ:圧力波の往復時間
La:配管長 [m]
a:圧力伝播速度 [m/s]
バルブの有効ストローク時間の計算
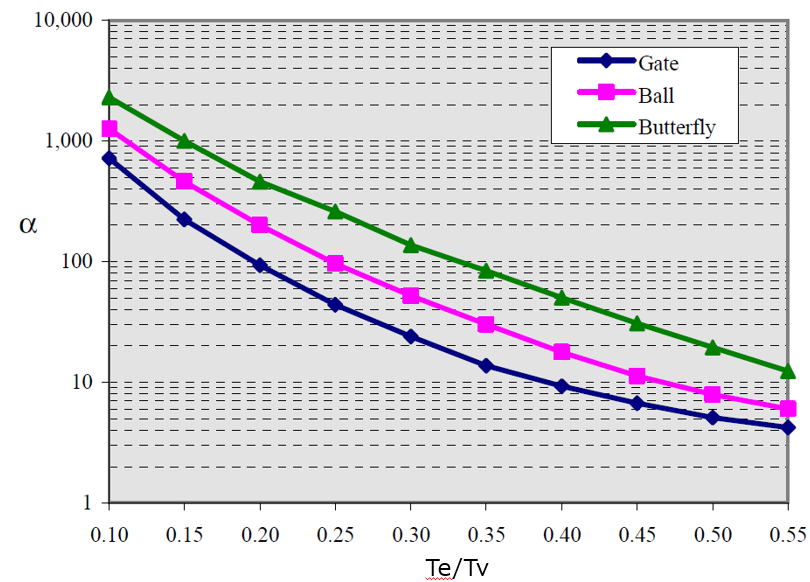
$$α=\biggl(\frac{A_v}{A_p}\biggl)^2λ\frac{L_e}{D}$$
Av:バルブ呼び径における断面積 [m2]
Ap:配管断面積 [m2]
Le:配管相当長 [m]
D:配管内径 [m]
λ:4f (f:ファニングの式における摩擦係数)
Tv:バルブのストローク時間(弁閉鎖時間)[s]
Te:バルブの有効ストローク時間(有効弁閉鎖時間)[s]
まず、上記のグラフの縦軸αから、バルブの有効ストローク時間Teとストローク時間Tvの比Te/Tvを読み取ります。読み取る対象のグラフはバルブの種類(ゲート弁、ボール弁、バタフライ弁)によって変わります。
実際のストローク時間Tvはバルブのデータシートなどから引用します。
急閉鎖/緩閉鎖の判定
上記で算出した「圧力波の往復時間:μ」と「バルブの有効ストローク時間:Te」を比較します。
μ>Teであれば急閉鎖
μ<Teであれば緩閉鎖
となります。
急閉鎖の場合
急閉鎖の場合はJoukowsky式(ジューコフスキーの式)を使用して水撃圧を計算します。
<Joukowskyの式>
$$ΔH=\frac{aΔV}{g}$$
ΔH:水撃圧(ウォーターハンマー発生時の上昇圧力) [m]
ΔV:流体の線速 [m/s]
a:圧力伝播速度 [m/s]
g:重力加速度 [m/s2]
さらに、ポンプの締め切り圧力と吸込み圧力を考慮する必要があるので、最大水撃圧Hmaxは以下の式から算出されます
$$H_{max}=ΔH+P_{shut}+P_{suc}$$
Hmax:最大水撃圧 [m]
ΔH:水撃圧(ウォーターハンマー発生時の上昇圧力) [m]
Pshut:ポンプ締め切り圧力 [m]
Psuc:吸込み圧力 [m]
Joukowskyの式は弁閉鎖の場合だけでなく、他の要因で液流量が短時間で変化する場合でも適用可能です。
緩閉塞の場合
緩閉鎖の場合はAllievi式(アリエビの式)を使用して水撃圧を計算します。
<Allieviの式>
$$ΔH=\frac{n}{2}(n+\sqrt{n^2+4})H_0$$
$$n=\frac{LΔV}{gH_0T_e}$$
ΔH:水撃圧(ウォーターハンマー発生時の上昇圧力) [m]
ΔH0:静水頭圧 [m]
g:重力加速度 [m/s2]
ΔV:流体の線速 [m/s]
Te:バルブの有効ストローク時間(有効弁閉鎖時間)[s]
よって、最大水撃圧Hmaxは以下の式から計算されます。
$$H_{max}=ΔH+H_0$$
Hmax:最大水撃圧 [m]
ΔH:水撃圧(ウォーターハンマー発生時の上昇圧力) [m]
ΔH0:静水頭圧 [m]
Allievi chartを用いる場合
Allievi chartを用いて水撃圧を求める方法についても解説します。
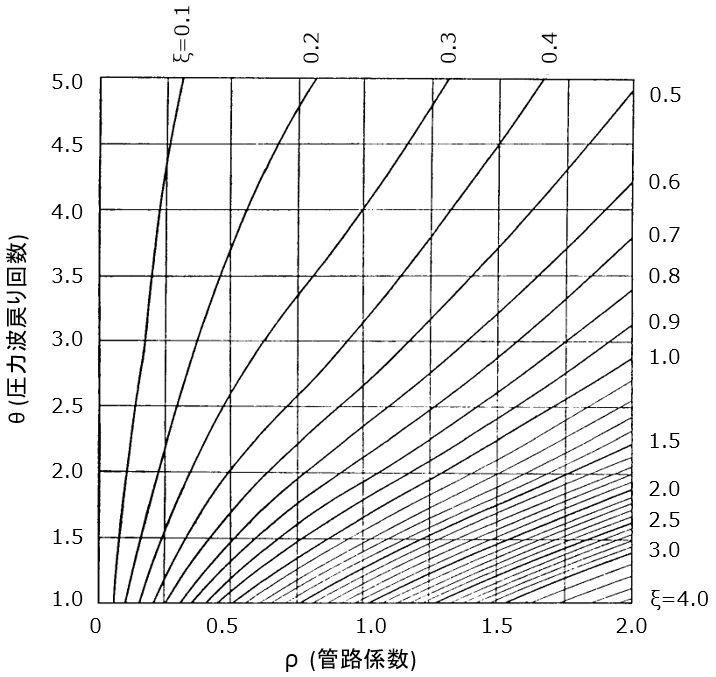
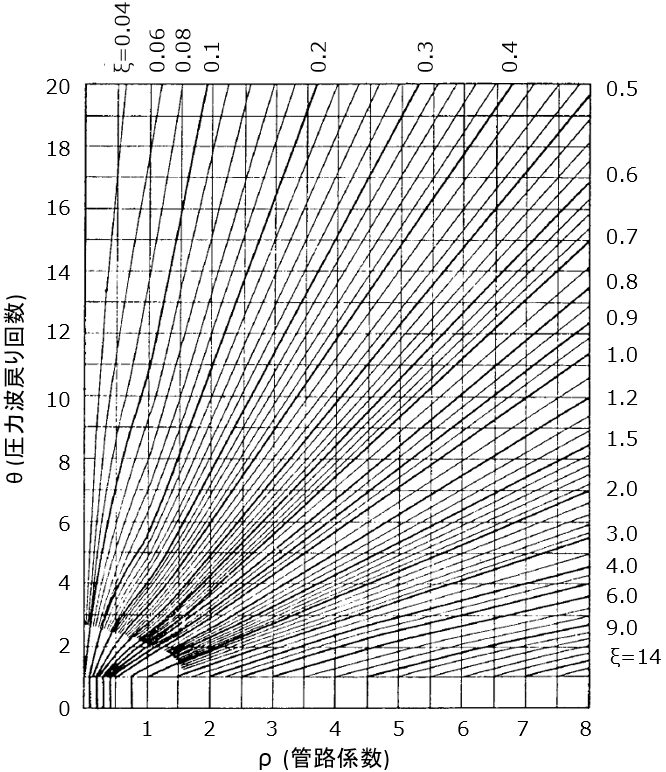
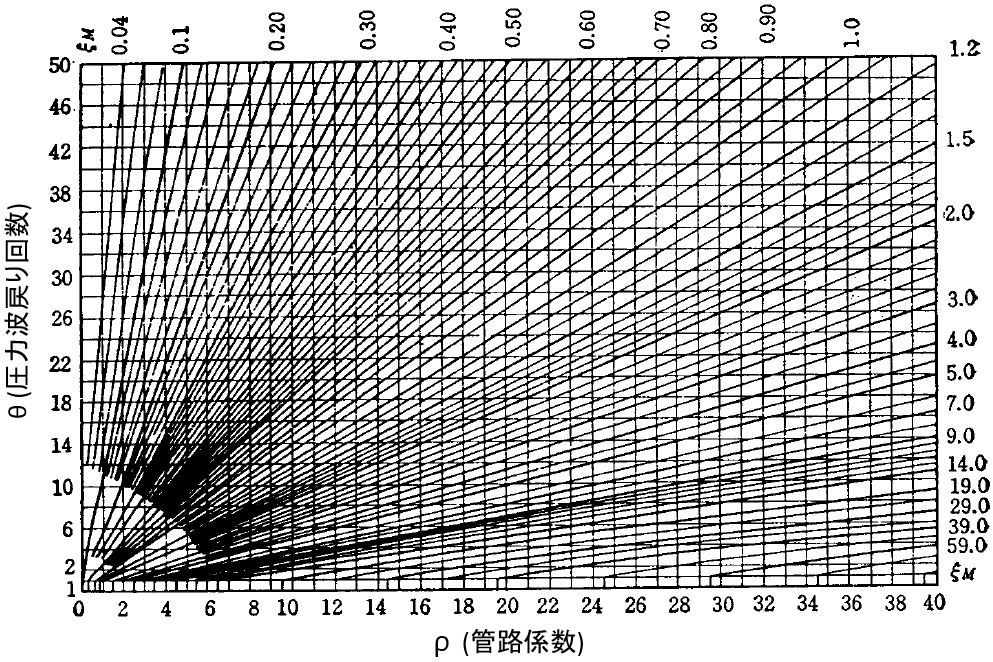
$$ρ=\frac{aΔV}{2gH_0}$$
$$θ=\frac{T_e}{μ}$$
$$H_{max}=H_0(1+ξ)$$
ρ:管路係数
a:圧力伝播速度 [m/s]
ΔV:流体の線速 [m/s]
ΔH0:静水頭圧 [m]
g:重力加速度 [m/s2]
θ:バルブ閉鎖までの圧力波戻り回数
μ:圧力波の往復時間
Te:バルブの有効ストローク時間(有効弁閉鎖時間)[s]
ξ:Allievi chart定数
Hmax:最大水撃圧 [m]
管路係数ρとバルブ閉鎖までの圧力波戻り回数θを求め、上図のAllievi chartから定数ξを読み取ります。
さらに定数ξと静水頭H0から最大水撃圧Hmaxを算出することができます。
なお、θ≦1.0の場合は急閉鎖に該当するので、前項のJoukowskyの式で最大水撃圧を計算します。
計算例
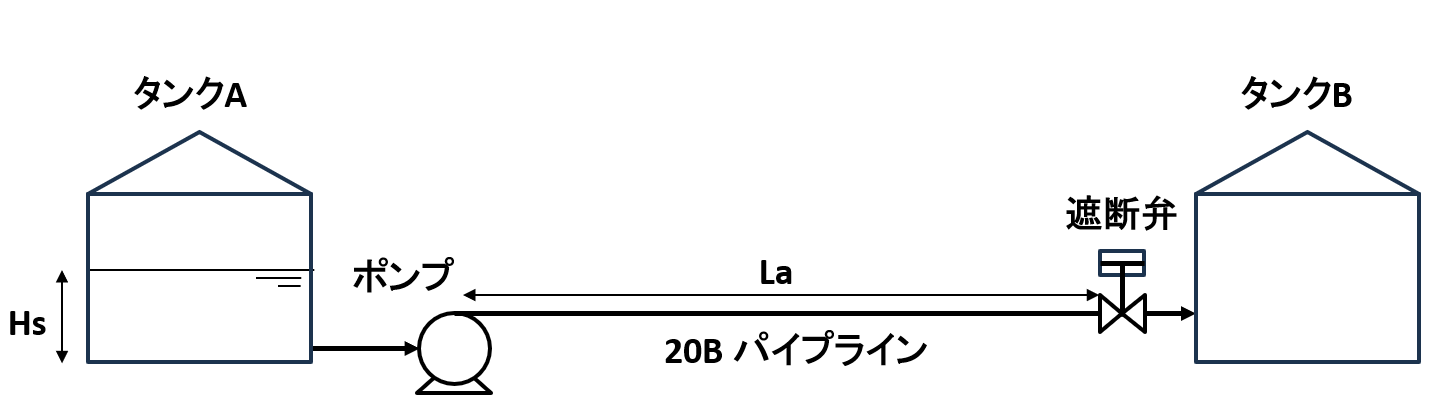
上図のように液体(今回はLNG)をタンクAからタンクBまでパイプラインで輸送する系を考えます。パイプラインにはタンクB近傍に遮断弁が設置されており、送液中に遮断弁が閉じてしまった場合に発生する最大水撃圧力を計算します。
水撃圧を計算する上で与えられている情報は以下の通りです。
La:配管長 = 1500 m
D:配管内径 = 0.5 m
t:配管肉厚 = 7.92 mm
E:配管材のヤング率 = 2.1×10^10 kgf/m2
λ:摩擦係数 = 0.0156
Tv:遮断弁のストローク時間(弁閉鎖時間)= 30秒(20Bのゲート弁想定)
γ:LNG密度 = 463 kg/m3
K:LNGの体積弾性係数 = 1.265×10^8 kgf/m2
Q:流量 = 0.633 m3/s
Hs:タンクAの水頭圧 = 1 m
Hd:ポンプ締め切りヘッド = 112 m
H0:遮断弁入側の水頭圧 = 89.2 m
まず、圧力伝播速度aを計算します。
$$a=\frac{1}{\sqrt{γ\bigl(\frac{1}{K}+\frac{1}{E}\frac{D}{t}C\bigl)}}$$
に代入するとa=445 m/sとなります。
次に圧力波の往復時間μは
$$μ=\frac{2L_a}{a}$$
に代入して計算すると、μ=6.74 秒となります。
また、配管径と同じサイズのゲート弁なので、Av/Ap=1として遮断弁の有効ストローク時間Teを計算すると、
$$α=\biggl(\frac{A_v}{A_p}\biggl)^2λ\frac{L_e}{D}$$
に代入して、α=46.8となるため、グラフからTe/Tvを読み取って、Te=7.2秒となります。
ここで、圧力波の往復時間μと有効ストローク時間Teとを比較すると、μ<Teなので、緩閉鎖となります。
管路係数ρと圧力波戻り回数θをそれぞれ計算すると、
$$ρ=\frac{aΔV}{2gH_0}$$
$$θ=\frac{T_e}{μ}$$
に代入して、ρ=0.82、θ=1.1となります。
これをもとにAllievi chartからAllievi chart定数ξを読み取ると、ξ=1.8となります。
よって、
$$H_{max}=H_0(1+ξ)=89.2(1+1.8)=249.76$$
となり、最大水撃圧Hmax = 249.76 mと算出することができました。
パイプラインの設計圧力はこの水撃圧を考慮したものでなければなりませんが、今回の計算例では最大水撃圧がポンプの締め切り圧力と比較して大きいため、設計圧力を決定する際は要注意です。
主な対策
主な対策は以下の通りです。
バルブ急閉鎖への対策
・バルブストローク時間を長くする
・バルブのタイプ変更
・配管流速を下げる
・圧力逃し弁の設置
・バッファードラム(サージドラム)設置
・配管長さをできるだけ短くする
ポンプ急停止への対策
・ポンプの圧力制御システムの見直し
・モーターのフライホイール(GD^2)を増加させる
・逆止弁をノンスラムタイプに変更
・逆止弁周りにバイパスラインを設置
・バッファードラム(サージドラム)設置
・バキュームブレーカー設置
液柱分離への対策
・バルブストローク時間を長くする
・モーターのフライホイール(GD^2)を増加させる
・バッファードラム(サージドラム)設置


