「トルートンの規則」「Guldbergの通則」とは？蒸発熱、臨界温度の簡単な推算方法について解説

今回の記事では沸点から蒸発熱、臨界温度を簡単に求める方法として、「トルートンの規則」と「Guldbergの通則」について解説します。

トルートンの規則やGuldbergの通則を知っておくことで、沸点さえ分かれば、暗算や電卓で蒸発熱や臨界温度を簡単に計算することができます。

物質の蒸発熱や臨界温度はプロセスシミュレーターを用いることで計算することが可能ですが、いつでも使えるという訳ではなく、現場のトラブル対応や会議の場では、使えるツールはせいぜい電卓程度です。

そのような打ち合わせの場では、プロセスエンジニアに対しておおよその値はどれくらいかを尋ねる機会が多くありますが、これらの規則を知っていれば、その場で計算して回答することが出来ます。

素早く物性推算するためのツールの一つとして、プロセスエンジニアなら知っておきたい法則です。

トルートンの規則（Trouton's rule）

トルートンの規則はトルートンの通則とも呼ばれ、様々な種類の液体の沸点と蒸発熱との比がほぼ一定の値になる、という法則です。

数式で表すと以下の通りになります。

蒸発熱と沸点との比は、物質が非極性であれば20、極性物質であれば25の値となります。

■純物質におけるトルートンの規則【参考】

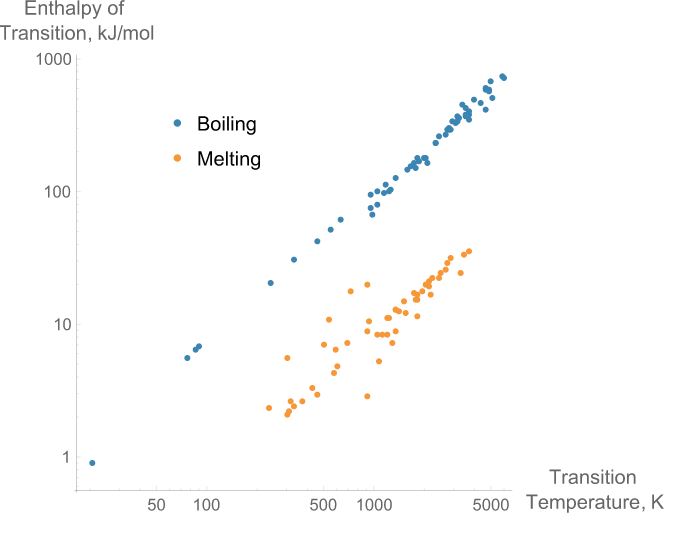
出典：Wikipedia

トルートンの規則は、ある物質の沸点さえ分かっていれば、その蒸発熱がすぐに推定できるので、非常に便利です。

もちろん、ある程度の誤差はありますが、現場や会議でおおよその値を推測する程度であれば十分な精度です。

ヒルデブランドの規則（Hildebrand rule）

ヒルデブランドの規則は、トルートンの規則同様に物質の沸点と蒸発熱との関係を示した規則ですが、トルートンの規則を修正したものです。

■トルートンの規則とヒルデブランドの規則の比較

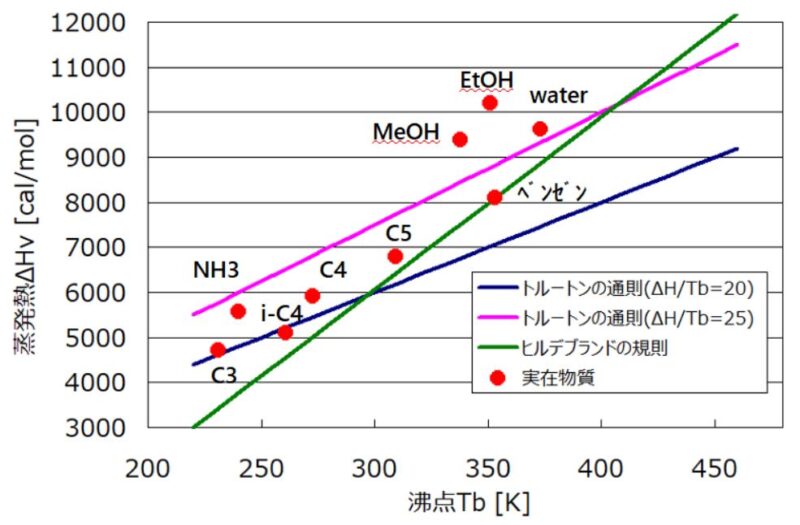
トルートンの規則とヒルデブランドの規則の比較を上記のグラフに示しました。

実際に使用する場合、精度良く計算可能なのはヒルデブランドの規則ですが、沸点に対する一次式を暗記しなければなりません。そのため、便利なのはシンプルな計算（沸点を20～25倍するだけで良い）で求めることが出来るトルートンの規則です。

トルートンの規則とヒルデブランドの規則はケースバイケースで使い分けるようにして下さい。

Guldbergの通則（Guldberg rule）

Guldbergの通則は、沸点と臨界温度との比がほぼ一定になる、という法則です。

数式で表すと以下の通りになります。

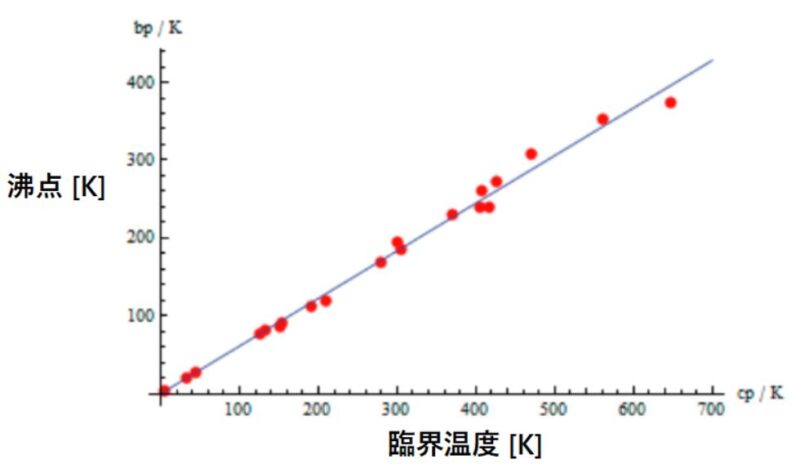
出典：信州大学講義資料

Guldbergの通則も非常にシンプルな式で、沸点と臨界温度との比がおよそ2：3になることを表しています。

誤差は±30%程度あるものの、その場で沸点から臨界温度を推測することができる、非常に便利な法則です。

まとめ

今回の記事では沸点から蒸発熱、臨界温度を求める方法として、「トルートンの規則」と「Guldbergの通則」について解説しました。

トルートンの規則やGuldbergの通則を知っておくことで、沸点さえ分かれば、暗算や電卓で蒸発熱や臨界温度を簡単に計算することができます。

現場のトラブル対応や会議の場では、プロセスエンジニアに対しておおよその値が尋ねられることがありますが、トルートンの規則やGuldbergの通則を知っていれば、その場で電卓を叩くことで、素早く物性推算することが可能です。

そのため、プロセスエンジニアなら知っておきたい法則です。

この記事が役に立てば幸いです。ではまた他の記事でお会いしましょう。