今回の記事では吸収塔高さの計算に必要な移動単位数(NTU)を図解法で求める方法について解説します。
気体中の特性成分を液体に溶解させて除去、回収する操作をガス吸収と呼びますが、最近では脱炭素の観点から、排ガス中の二酸化炭素を除去、回収する有効な手段（化学吸収法）として注目されています。
ガス吸収を行う機器は吸収塔と言われますが、で最も一般的な吸収塔の形式は充填塔です。
今回は充填塔に代表される、ガス吸収塔の設計、特に塔高さを計算するために必要な移動単位数（NTU）の図解法による算出方法について解説します。
合わせて読みたい
・化学工学ってプラントエンジニアリングのどんな場面で使われる？
・【蒸留塔】棚段塔はどんな構造？棚段塔の構造・特徴と運転範囲について解説
・【蒸留塔】充填塔と棚段塔は何が違う？充填塔の構造・特徴について解説
・【蒸留塔】棚段塔・充填塔の設計手順、データシート作成方法の解説
・【蒸留塔】簡単に蒸留分離段数の目安を計算する方法の解説
・ブルー水素、グリーン水素って何？プラントエンジニアが技術のキーポイントを解説
・ブルーアンモニアは実用化済み？プラントエンジニアがブルーアンモニア、グリーンアンモニアを解説
・【ブルー水素】伊藤忠はなぜエアリキード社と組んだのか？国内最大の水素製造プラント建設プロジェクト
・水素は減圧すると温度が上昇する？知っておくべき圧縮水素の物性について解説
・脱炭素のキーテクノロジー！二酸化炭素の分離回収技術の解説
・オルト水素、パラ水素とは？液化水素プラントの設計で知っておくべき物性について
・【気液平衡】プラント設計で使用される気液平衡の推算モデルの解説
・【移動現象】粒子の抵抗係数と終端速度の計算方法の解説
・【回転機】真空ポンプの排気時間の計算方法の解説
・タンク、ベッセルの排水時間の計算方法の解説
・【撹拌】Pv値とは？攪拌槽のスケールアップの留意点について解説
・【物性推算】沸点から蒸発熱、臨界温度を求める方法。「トルートンの規則」と「Guldbergの通則」について解説
・【物性推算】プロセスシミュレーションで使用される物性推算モデルの適用範囲の解説
・サットンの式とは？毒性ガス、可燃性ガスの着地濃度の計算方法について解説
・プロセスシミュレーションのモデリングにおける各機器の圧力損失の設定方法
・プラントのプロセス制御性と最適な制御方式の考え方について解説
移動単位数（NTU）とは
気液などの二相間で物質移動（吸収など）を行う場合、物質移動の難易を示す尺度が移動単位数（Number of Transfer Unit：NTU）です。
NTUが小さければ物質移動は容易、大きければ困難であることを示します。
また、NTUは吸収塔の高さを計算するために使用される無次元量です。
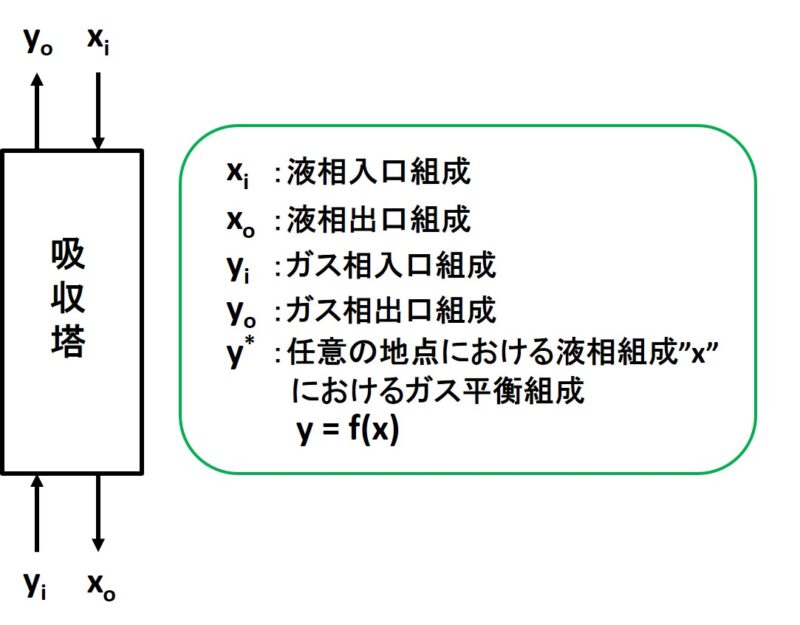
上記のような吸収塔において、塔高さZ[m]は次の式で表されます。
$$Z=K×{NTU}$$
ただし、
$$K=\frac{G}{k_{y}aS}$$
$${NTU}=\int_{y_i}^{y_o}\frac{dy}{y^*-y}$$
Z：吸収塔高さ [m]
K：有効推進力
NTU：移動単位数
G：ガス流量 [mol/s]
kya：総括移動容量係数 [mol/m3s]
S：塔断面積 [m2]
yi：ガス相入口組成
yo：ガス相出口組成
y*：任意の地点の液相組成xにおけるガス平衡組成
少し式形が複雑ですが、吸収塔の高さは有効推進力とNTUをかけ合わせたもの、ということになります。
つまり、NTUが大きくなると吸収塔の高さが高くなってしまうため、プラント設計が難しくなることを意味します。
NTUの計算（図式積分）
NTUを算出するためには、以下の積分を解かなければなりません。
$${NTU}=\int_{y_i}^{y_o}\frac{dy}{y^*-y}・・・①$$
ここで、ガスの出口組成yoと入口組成yiとの関係がyo<<yiであることから、yo-yo*<<yi-yi*なので、逆数をとると、
$$\frac{1}{y_o-{y_o}^*}>>\frac{1}{y_i-{y_i}^*}$$
となるため、①式の被積分関数は下図のようになります。
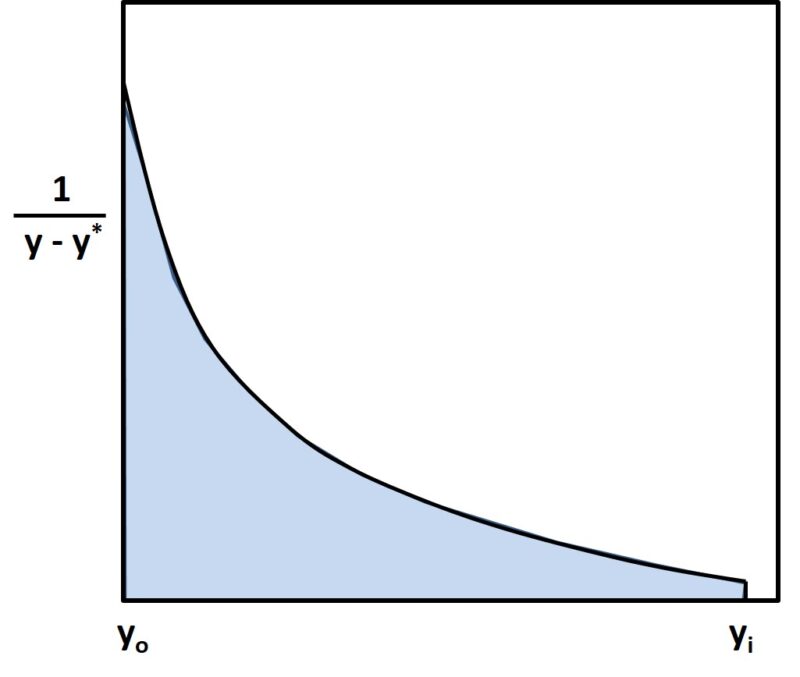
上図の水色部の面積を計算すればNTUが計算できますが、このような形の図式積分は簡単ではありません。
式変形
しかし、NTUを計算しやすくするための方法として、次のような手順があります。
$$d(\ln{y})=\frac{dy}{y}$$
であることを利用すると、
$$\frac{1}{y-y^*}dy=\frac{y}{y-y^*}d(\ln{y})$$
となるため、
①式は次のように変形されます。
$${NTU}=\int_{\ln{y_o}}^{\ln{y_i}}\frac{y}{y^*-y}d(\ln{y})・・・②$$
このように変形することで、下図のようになります。
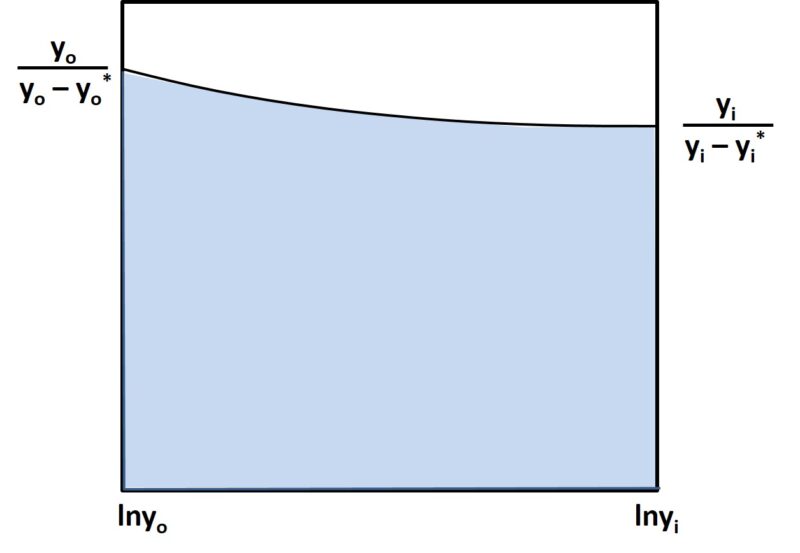
上図の水色部分を計算することでNTUが求まりますが、この積分面積がほぼ台形となるため、計算がしやすくなります。
このように処理することで、例えばyとxの関係が非線形の場合（y=mxの関係で表せられないような場合）でも手計算でNTUを計算することが可能です。
図解法によるNTUの計算
ここから、図解法によりNTUを計算します。
まず、下図のように前項の面積をn等分に分割します。
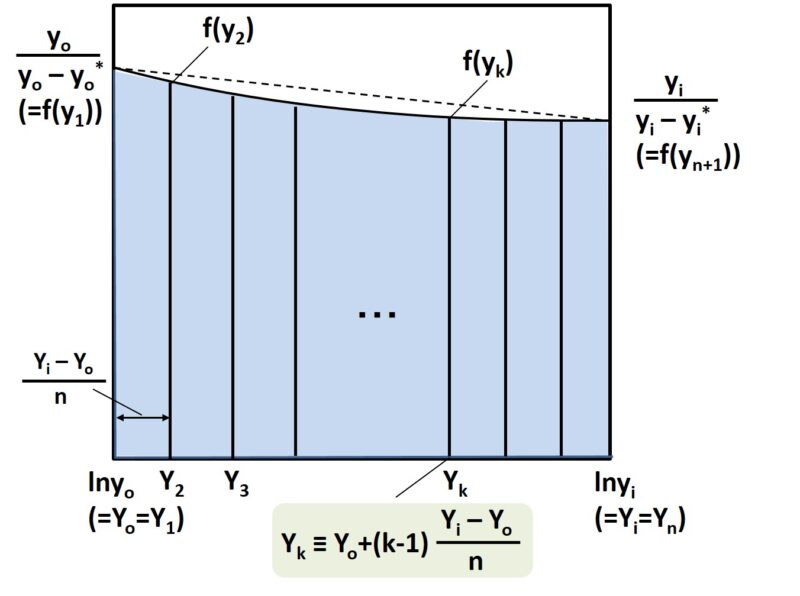
基本的な手順としては、n等分したそれぞれの図形を台形とみなし、それぞれの台形の面積を足し合わせることでNTUを計算します。
$$Y=\ln{y}$$
と置くと、
n等分した１つ目の横軸の座標はY1(=Yo=lnyo)、2つ目の座標はY2、、、とすると、k番目の横軸の座標はYkとなります。
各台形の幅は、
$$\frac{Y_i-Y_o}{n}$$
なので、YkをYiとYoを用いて表すと
$$Y_k=Y_o+(k-1)\frac{Y_i-Y_o}{n}$$
となります。例えば、5等分した場合の4つめの座標Y4は
$$Y_4=Y_o+3\frac{Y_i-Y_o}{5}$$
となります。
よって、それぞれの横座標Y(=lny)における縦座標f(y)（下式）を求めておけば、それぞれの台形の面積の和を計算することができます。
$$f(y)=\frac{y}{y-y^*}$$
※y*は液相組成xのガス平衡組成なので、液相組成から求まる。
台形の面積は「(上底＋下底)×高さ÷2」で求まるため、NTUを求めるための計算式は次の通りです。
※数式表示が途切れている場合はスライドすると表示されます。
ただし、
$$y_1=y_o、y_{n+1}=y_i$$
上記はn等分した時のNTUの計算式ですが、解析解と比較してn=5でも誤差は1%程度で、n=3でも1%～数%程度です。
最も簡便なNTU計算法
最も簡便にNTUを計算する方法として、図形全体を一つの台形とみなし（分割しない）、その台形の面積を計算する方法があります。
この時、NTUを求めるための計算式は次の通りです。
$${NTU}=\frac{1}{2}\biggl(\frac{y_i}{y_i-{y_i}^*}+\frac{y_o}{y_o-{y_o}^*}\biggl)\times\ln{\frac{y_i}{y_o}}$$
この方法だと、誤差は数%程度になりますが、プラント設計初期に吸収塔高さを計算する上では十分な精度です。
NTU計算例
例題として、ある吸収塔のNTUを計算します。
3等分する場合と図全体と台形とみなす場合（分割無し）の2通りで計算します。
前提条件は次の通りとします。
前提条件
ガス相入口組成：yi=0.04
ガス相出口組成：yo=0.001
液相入口組成：xi=0.005
気液比：α=4（一定）
ヘンリー定数：m=0.08（一定）
3等分の場合
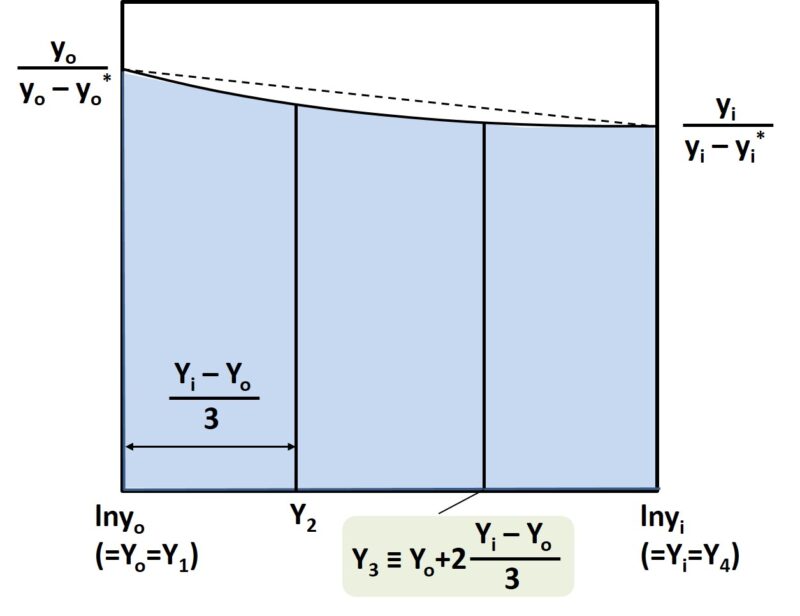
※数式表示が途切れている場合はスライドすると表示されます。
$$Y_o=Y_1=\ln{y_o}=-6.90776$$
$$Y_i=Y_4=\ln{y_i}=-3.21888$$
$$Y_2=\frac{2Y_o+Y_i}{3}=-5.67813$$
$$Y_3=\frac{Y_o+2Y_i}{3}=-4.4485$$
また、y=exp(Y)なので、
前提条件より、
$$y^*=mx=0.08x$$
なので、y*及びf(y)=y*/(y-y*)を求めると、
$$f(y_1)=\frac{y_1}{y_1-{y_1}^*}=1.666667$$
$$f(y_2)=\frac{y_2}{y_2-{y_2}^*}=1.522979$$
$$f(y_3)=\frac{y_3}{y_3-{y_3}^*}=1.485531$$
$$f(y_4)=\frac{y_4}{y_4-{y_4}^*}=1.474926$$
よって、NTUを計算すると、
となり、この前提条件での吸収塔の移動単位数NTUは5.63と計算することが出来ました。
台形とみなす場合（分割無し）
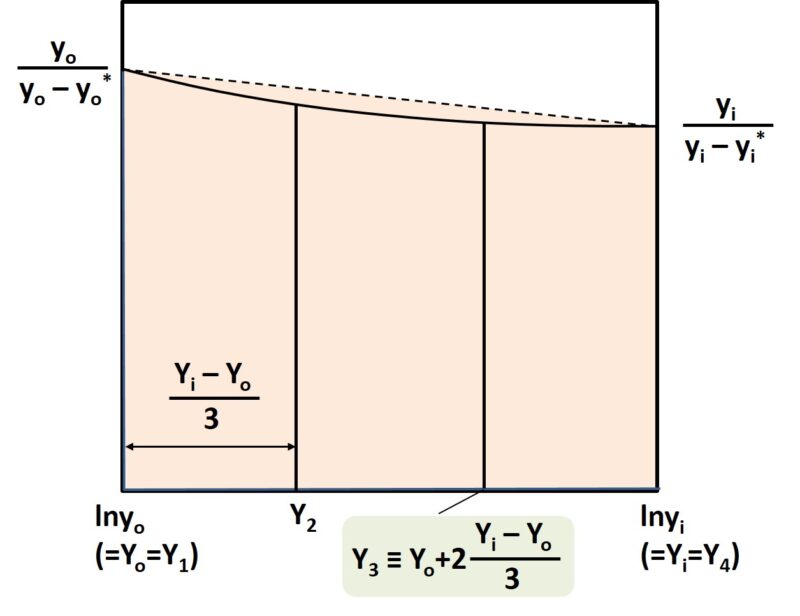
上図の着色部の面積を求めます。
前提条件より、NTUを計算すると、
となり、移動単位数NTUは5.73と計算することが出来ました。
3等分してNTUを計算した時と比べても、それほど差異は大きくないことがわかります。
まとめ
今回の記事では吸収塔高さの計算に必要な移動単位数(NTU)を図解法で求める方法について解説しました。
気体中の特性成分を液体に溶解させて除去、回収する操作をガス吸収と呼びますが、最近では脱炭素の観点から、排ガス中の二酸化炭素を除去、回収する有効な手段（化学吸収法）として注目されています。
ガス吸収は充填塔に代表される吸収塔により行われます。今回はその吸収塔の設計、特に塔高さを計算するために必要な移動単位数（NTU）の図解法による算出方法について解説しました。
分割数を大きくすればするほど精度は高くなりますが、その分計算の手間は大変です。一般的には分割は3~5程度で十分で、特にプラント設計初期では分割をしなくても十分な精度となることが多いです。
この記事が役に立てば幸いです。ではまた他の記事でお会いしましょう。
